跳转至

Transformer Model

Tip

推荐一个很直观的 Transformer 可视化交互网站：Transformer Explainer。

本文介绍 Transformer 模型的基本原理。

产生背景

在 使用 RNN 进行文本生成任务 时，RNN 由于只能按时间步串行计算，导致：

  • 信息量上：所有信息被压缩进单一隐状态，在长距离信息传递时导致信息量急速衰减；
  • 扩展性上：无法充分利用 GPU 的并行特性，训练缓慢，难以扩展到大型模型。

Attention Is All You Need 应运而生。其提出的 Transformer 网络架构让序列中任意两个 token 可以直接交互，不再依赖顺序递推结构，做到了并行计算，从而可以狠狠地堆网络深度，从根本上提升了建模效率与表达能力。

模型结构

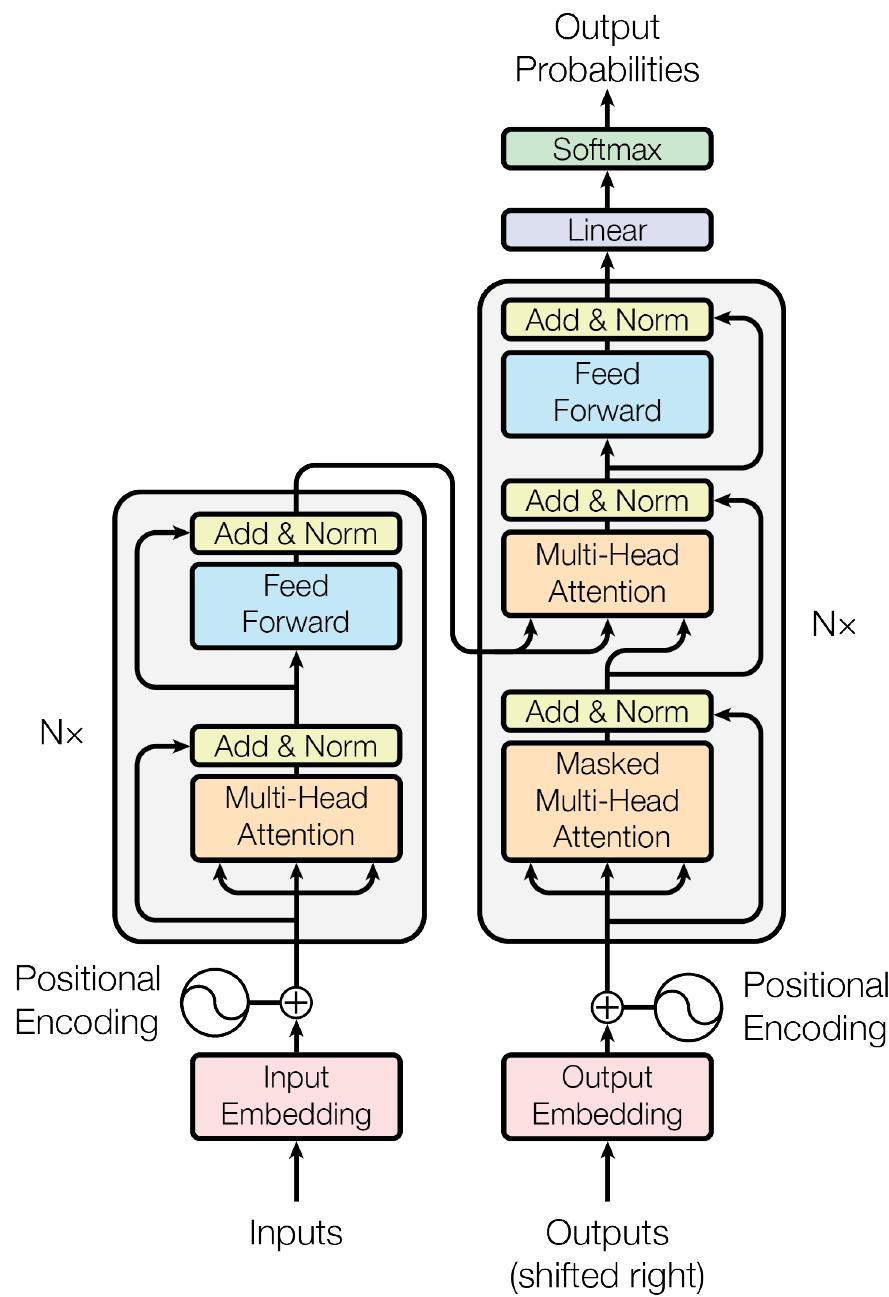
Transformer 由 Encoder-Decoder 结构组成，每个部分包含多个堆叠的 Block。每个 Block 内部均采用一致的模式：注意力机制、前馈网络、残差连接、层归一化。整体架构如下图所示：

Transformer 模型架构

可以抽象为下图：

flowchart TD
    A[Input text] --> B[Tokenization]
    B --> C[Word embedding]
    B --> D[Positional encoding]
    C --> E[Transformer block]
    D --> E
    E --> F[Output text]

    subgraph E[Transformer block]
        direction LR
        E1[Attention mechanisms]
        E2[Feedforward neural network]
        E3[Normalization layer]
    end

数据流向

训练阶段，输入序列与目标序列（右移一位）同时输入模型。Encoder 负责构建输入序列的上下文表示，Decoder 通过 Masked Self-Attention 仅观察到历史 token，从而计算条件概率 \(p(y\mid x)\)，最终组合损失 \(\,\text{loss}=-\log p(y\mid x)\,\)。

推理阶段，Decoder 只能看到已生成的 token，每生成一个新的 token 即重新参与一次前向运算。因果 Mask 保证生成过程满足自回归约束。

Positional Embedding

Transformer 无递归结构，无法内建位置信息，必须显式提供。

论文提出正弦位置编码：

\[ \begin{aligned} \text{PE}_{(pos,2i)}=\sin\left(\frac{pos}{10000^{2i/d}}\right) \\ \text{PE}_{(pos,2i+1)}=\cos\left(\frac{pos}{10000^{2i/d}}\right) \end{aligned} \]

特性包括：

  • 可外推（序列变长仍能使用）
  • 可微、周期性强
  • 不增加额外参数

工程中也可以选择训练型位置向量，将其直接加入 token embedding。

Multi-Head Attention

多头注意力通过为每个 token 生成 \(Q,K,V\)，再按头划分多个独立子空间捕获不同关系模式。整体公式为：

\[ \text{MHA}(X)=\text{Concat}(h_1,\ldots, h_H)W_O \]

每个头独立计算注意力，从而提升多尺度、多关系的表达能力。

注意力的核心计算方式是缩放点积 (Scaled Dot-Product Attention)：

\[ \text{Attention}(Q, K, V)=\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \]

缩放因子 \(\sqrt{d_k}\) 用于抑制高维向量点积的数值爆炸，使 softmax 保持稳定。

Encoder 的 Self-Attention 不需要 Mask，所有 token 可以进行全局交互，从而捕获输入序列中的长依赖。该模块在每个 Encoder Block 都会重复出现，使表示不断强化。

Masked Multi-Head Attention

Decoder 必须保证只使用已生成的历史 token，因此注意力矩阵中未来位置会被替换为 \(-\infty\)，经 softmax 后权重为 \(0\)，从而实现因果性。

Masked Multi-Head Attention 的计算与普通 Attention 相同，但输入矩阵中会添加因果 Mask：

  • 上三角区域被抑制
  • 保证自回归生成流程合法

Cross Attention

Decoder 获取输入序列信息的关键模块。其输入 \(Q\) 来自 Decoder，\(K,V\) 来自 Encoder。作用如下：

  • 建立输出与输入的跨序列对齐
  • 捕获翻译等任务中的对应关系
  • 是连接 Encoder 表示与 Decoder 生成的唯一桥梁

Feed-Forward Network

每个 Block 中都有一个位置独立的前馈网络，用于局部非线性变换，从而确保网络的表示能力。常见形式是两层线性层加激活函数：

\[ \text{FFN}(x)=W_2\,\sigma(W_1\,x+b_1)+b_2 \]

通常 \(W_1\) 会将维度扩展为原来的 \(4\) 倍，再缩回原维度，以增强表示能力。

Residual & LayerNorm

每个子层（注意力层、FFN）外部都包裹残差连接和层归一化：

  • 残差连接让梯度传播路径更短，更稳定
  • LayerNorm 保持数值稳定，使训练更快收敛

典型结构：

  • Pre-LN：先归一化，再进入子层（现代模型更常用）
  • Post-LN：子层后归一化（原论文形式）

Dropout

注意力权重、FFN 输出、残差路径都会用到 dropout，减少过拟合，有助于稳定训练。

性能分析

假设某个句子 S 的 token 数为 \(n\)，模型嵌入维度为 \(d\)（由于 \(n\) 往往远大于 \(d\)，所以我们认为 \(n\) 为变量，\(d\) 为常量）。

计算 \(Q,K,V\) 矩阵：

  • \(n\) 个 token 的嵌入表示为 \(X_{n\times d}\)，\(W_Q,W_K,W_V\) 的维度均为 \(d\times d\)，那么 \(Q_{n\times d}=XW_Q\) 就需要 \(nd^2\) 次运算，时间复杂度为 \(O(n)\)；
  • \(K\) 和 \(V\) 的运算同理。

计算注意力分数：

  • 对于 \(\frac{QK^\top}{\sqrt{d_k}}\)，需要进行 \(n^2d\) 次运算，时间复杂度为 \(O(n^2)\)；
  • softmax 需要对 \(n\times n\) 的矩阵做归一化，时间复杂度为 \(O(n^2)\)；
  • 将归一化后的结果和 \(V\) 矩阵相乘，即 \(n\times n\) 与 \(n\times d\) 叉积得到 S 的 \(n\times d\) 的注意力分数矩阵，时间复杂度为 \(O(n^2)\)；
  • 将注意力分数过一个 \(d\to d\) 的线性层得到最终 \(n\times d\) 的输出，时间复杂度为 \(O(n)\)。

在不考虑多头机制（即会将 \(d\) 维划分为 \(h\) 个 \(d_h\)）的情况下，总时间复杂度为 \(O(n^2)\)。

代码实现

参考：