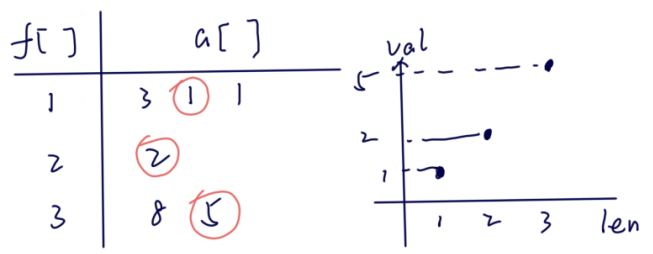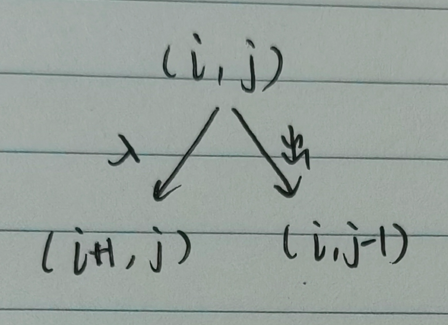动态规划
动态规划 (Dynamic Programming, DP) 算法是一种利用子问题的解来求解原问题的解的策略,本质是一种 DAG 上的运算。推荐阅读 动态规划杂谈 1 来对动态规划有一个更深刻的认知。
动态规划问题需要满足的基本条件:
- 通过实时存储子问的解,DP 算法在原问题有大量「重叠子问题」的情况下尤为有效;
- 当然,奏效的前提是原问题具有「最优子结构」的性质,即原问题可以被分解为多个子问题来求解;
- 同时,DP 算法还需要遵守「无后效性」原则,即当前问题依赖的子问题只能是已经被解决的问题,而不能是在未来才会被解决的问题。
在题目满足上述三个基本条件的前提下,DP 算法的核心有两点:
- 状态定义。如何合理定义问题,从而「完整表示」所有的状态?
- 状态转移。如何合理划分问题,从而「不重不漏」地基于子问题的解得到原问题的解?
本文将会围绕上面两个核心要点,介绍动态规划算法在各类问题下的经典模型。读者应当时刻牢记上述两个核心要点,逐步构建自己的动态规划理论体系。
*注:状态转移有「被动转移」与「主动转移」两种逻辑方向,但这仅仅是思考习惯的区别,本文将会全部使用前者。下图展示了两种转移策略的逻辑:
记忆化搜索¶
在开始学习 DP 之前,你一定做过类似于求斐波那契数列的问题,即有一个函数定义为:
你一定可以轻松地写出下面的搜索(递归)函数:
但是当 \(n\) 超过 \(30\) 以后,上面的程序就很难在你可忍受的时间内计算出结果了。此时就需要更高效的算法来求解这个问题。
你一定可以很轻松地看懂下面的程序:
bool vis[10];
int ans[10];
int f(int n) {
if (n == 1 || n == 2) {
return 1;
}
if (vis[n]) {
return ans[n];
}
vis[n] = true;
return ans[n] = f(n - 1) + f(n - 2);
}
大家习惯于将其称作 记忆化搜索,因为其本质上还是搜索,只不过将中间的计算结果利用 ans 数组保存起来了而已。当然,把记忆化搜索写在这里并不代表其仅局限于此,有些时候记忆化搜索甚至可以解决高难度的题目,或者有助于你思考出递推(动态规划)写法。
例:滑雪¶
经典之处:记忆化搜索板子题/写法
难度:洛谷 黄
OJ:洛谷
题意:给定一个 \(n\times m\ (1\le n,m \le 100)\) 的矩阵,现在可以从其中任意位置开始向上下左右四个方向移动,只能移动到比原来位置更小的地方。问最远移动距离是多少。
思路:
- 显然可以从每一个位置开始 DFS 并统计最长路径,如果用
dfs(i, j)表示从(i, j)出发可以走的最远路径长度,那么显然可以通过dfs(i, j) = max(dfs(i, j + 1), dfs(i, j - 1), dfs(i - 1, j), dfs(i + 1, j)) + 1来递归计算。但是这样做的时间复杂度为 \(O(n^2m^2)\),无法通过本题; - 从上述过程朴素策略可以发现,
dfs(i, j)会被多次调用,并且 其值一旦计算出来后续都不会被改变,也就是说我们重复计算了dfs(i, j)的值,因此我们将其预先存储起来,后续取出就只需要 \(O(1)\) 的计算开销了。
时间复杂度:\(O(nm)\)
from functools import cache
MII = lambda: map(int, input().strip().split())
n, m = MII()
g = [list(MII()) for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]
@cache # 记忆化就这一行,Python 最低版本为 3.9
def dfs(i: int, j: int) -> int:
res = 0
for k in range(4):
ni = i + dx[k]
nj = j + dy[k]
if 0 <= ni < n and 0 <= nj < m and g[i][j] > g[ni][nj]:
res = max(res, dfs(ni, nj))
return res + 1
ans = 1
for i in range(n):
for j in range(m):
ans = max(ans, dfs(i, j))
print(ans)
#include <iostream>
#include <set>
using namespace std;
const int N = 110, M = 110;
int n, m;
int g[N][M];
int f[N][M]; // 记忆化数组
bool vis[N][M]; // 标记是否访问过
int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, 1, -1};
int dfs(int i, int j) {
if (vis[i][j]) {
return f[i][j];
}
vis[i][j] = true;
int res = 0;
for (int k = 0; k < 4; k++) {
int ni = i + dx[k], nj = j + dy[k];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && g[i][j] > g[ni][nj]) {
res = max(res, dfs(ni, nj));
}
}
return f[i][j] = res + 1;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> g[i][j];
}
}
int ans = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
ans = max(ans, dfs(i, j));
}
}
cout << ans << "\n";
return 0;
}
线性 DP¶
现在仍然要求解斐波那契数列,你一定可以很轻松地看懂下面的程序:
int f(int n) {
int f[n + 1] {};
f[1] = f[2] = 1;
for (int i = 3; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
大家习惯于将其称作 递推,因为每一个结果都是「基于相邻子结果」推导而来,当然这其实就是线性 DP,只不过线性 DP 不局限于从相邻状态转移的情况。
注意:
- 子数组/子串是连续的;
- 子序列可以不是连续的。
例:牛的语言学¶
经典之处:从 DFS 优雅地过渡到递推
难度:CF 1600 *
OJ:AcWing
题意:给定一个字符串 \(s\ (5\le \lvert s\rvert \le 10^4)\),其由前段的单个词根和后段的多个词缀构成。词根的长度至少为 \(5\),单个词缀的长度 \(\in \{2,3\}\) 同时不允许相同的词缀连续出现。问 \(s\) 一共存在多少种可能的词缀?按照字典序输出所有可能的词缀。
思路:
- 由于词根只要长度满足就合法,因此我们应当从字符串的右侧开始枚举词缀。显然可以使用 DFS 枚举所有可能的词缀,时间复杂度为指数级,过不了本题。详情见下方 DFS 代码;
- 又由于一个词缀能否合法存在取决于右侧词缀的状态,因此也可以从右到左进行递推。我们约定字符串下标从 \(0\) 开始,切片为左闭右开。则有如下状态定义与状态转移:
- 状态定义:我们定义 \(ok_i\) 表示字符串 \(s\) 以下标 \(i\) 结尾的词根能否合法存在,为
true表示可以,为false表示不可以; - 状态转移:判断以下标 \(i\) 结尾的词根能否合法存在,其实就是判断其后的第一个词缀 now 能否合法存在。而 now 能合法存在的前提是当 now 为词根部分时,其后部分也能够以词缀的形式存在,即
ok[i + len(now)] = true,在满足该前提之下想要让 now 合法存在只有两个场景:要么 now 与其后紧邻的一个长度相等的词缀 latter 不相同;要么 now 后面存在一个与其长度不等的合法词缀状态,即ok[i + 5] = true。
- 状态定义:我们定义 \(ok_i\) 表示字符串 \(s\) 以下标 \(i\) 结尾的词根能否合法存在,为
时间复杂度:\(O(n \log n)\)
s = input().strip()
d = {}
n = len(s)
ok = [False] * (n + 10)
ok[n - 1] = True
for i in range(n - 1, 3, -1):
for x in (2, 3):
now = s[i + 1:i + x + 1]
latter = s[i + x + 1:i + 2 * x + 1]
if ok[i + x] and (now != latter or ok[i + 5]):
ok[i] = True
d[now] = True
print(len(d))
for t in sorted(d.keys()):
print(t)
#include <iostream>
#include <set>
using namespace std;
string s;
set<string> se;
void dfs(int r, string latter) {
for (int x = 2; x <= 3; x++) {
int l = r - x;
if (l < 5) {
continue;
}
// 当前词缀为 s[l:r] 左闭右开
string now = s.substr(l, x);
if (now != latter) {
se.insert(now);
dfs(l, now);
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> s;
dfs(s.size(), "");
cout << se.size() << "\n";
for (auto t: se) {
cout << t << "\n";
}
return 0;
}
#include <iostream>
#include <set>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
string s;
cin >> s;
int n = s.size();
bool ok[n + 10] {};
ok[n - 1] = true;
set<string> se;
for (int i = n - 1; i >= 4; i--) {
for (int x = 2; x <= 3; x++) {
string now = s.substr(i + 1, x);
string latter = i + x + 1 < n ? s.substr(i + x + 1, x) : "";
if (ok[i + x] && (now != latter || ok[i + 5])) {
se.insert(now);
ok[i] = true;
}
}
}
cout << se.size() << "\n";
for (auto t: se) {
cout << t << "\n";
}
return 0;
}
例:Block Sequence¶
经典之处:倒序 DP 思维
难度:CF 1500
OJ:CF
题意:给定一个长为 \(n\ (1\le n\le 2\times 10^5)\) 的数组 \(a\ (1\le a_i \le 10^6)\),问最少删除其中的几个元素,使得最终的数组可以被划分为连续的子数组且每一个子数组的元素个数均为「子数组首元素数值 \(+1\)」的形式。
思路:每一个元素 \(a_i\) 都有删与不删两种状态,如果删除,没有影响,如果不删除,则表示以 \(a_i\) 为首元素的数组要合法存在。如果我们从左到右枚举,可以发现每一个元素都会影响右侧的状态且与左侧的状态毫无关系,但如果从右往左枚举就可以一步步依赖了。我们有如下的状态定义与状态转移:
- 状态定义:用 \(f_i\) 表示 \(a_{i\sim n-1}\) 合法存在需要删除的元素个数。注意,若下标从 \(0\) 开始,则 \(f_n\) 的状态也要存在并且初始化为 \(0\);
- 状态转移:对于 \(a_i\) 来说,如果删除,那么显然有 \(f_i=f_{i+1}+1\),如果不删除,那么显然有 \(f_i=f_{i+a_i+1}\),两者取最小值即可。
时间复杂度 \(O(n)\)
OUTs = []
for _ in range(int(input().strip())):
n = int(input().strip())
a = list(map(int, input().strip().split()))
f = [0] * (n + 1)
for i in range(n - 1, -1, -1):
f[i] = f[i + 1] + 1
if i + a[i] + 1 <= n: # 刚好取等表示子数组覆盖整个尾串
f[i] = min(f[i], f[i + a[i] + 1])
OUTs.append(f[0])
print('\n'.join(map(str, OUTs)))
#include <iostream>
#include <vector>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<int> f(n + 1);
f[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
f[i] = f[i + 1] + 1;
if (i + a[i] + 1 <= n) { // 刚好取等表示子数组覆盖整个尾串
f[i] = min(f[i], f[i + a[i] + 1]);
}
}
cout << f[0] << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
solve();
}
return 0;
}
例:汉诺塔问题¶
经典之处:分治问题转化为递推求解
三塔难度:CF 1000 *,四塔难度:CF 1500 *
汉诺塔问题非常之经典以至于很多教材都会提到,但是分治算法对初学者来说理解起来还是有一定难度的。该问题的意思是,有 n 个大小不一的圆盘自下而上从大到小依次放置在一座塔上,现在给了其他的塔,需要利用其他的塔将这些圆盘同样按照自下而上从大到小的顺序转移到另一座塔上。这里讲解含有三座塔以及四座塔的情况。
1)对于三座塔
思路:
- 记三座塔分别为 A、B 和 C,同时现在所有的圆盘都在 A 塔上。问题就抽象为了借助 B 塔将 A 塔的 n 个圆盘移动到 C 塔,将其方案数记作 \(f_n\);
- 我们首先肯定需要:1)借助 C 塔将 A 塔上方 n-1 个圆盘移动到 B 塔,2)然后把最大的那个圆盘移动到 C 塔,3)再借助 A 塔将 B 塔的 n-1 个圆盘移动到 C 塔。容易发现这是一个分治策略,第一步的方案数就是 \(f_{n-1}\),第二步的方案数就是 \(1\),第三步的方案数也是 \(f_{n-1}\)。于是我们就得到了递推公式:\(f_n=2\times f_{n-1}+1\),当然其实是从分治思想转化而来的;
- 结合 \(f_1=1\) 与 \(f_n=2\times f_{n-1}+1\),通过简单的推导可以得到 \(f_i=2^i-1\)。
时间复杂度:\(O(1)\),由于本题 OJ 中的 \(n\) 非常大,所以其实是 \(O(n)\) 的高精度。
#include <iostream>
#include <vector>
using namespace std;
class Int {
private:
int sign;
std::vector<int> v;
void zip(int unzip) {
if (unzip == 0) {
for (int i = 0; i < (int) v.size(); i++) {
v[i] = get_pos(i * 4) + get_pos(i * 4 + 1) * 10 + get_pos(i * 4 + 2) * 100 + get_pos(i * 4 + 3) * 1000;
}
} else {
for (int i = (v.resize(v.size() * 4), (int) v.size() - 1), a; i >= 0; i--) {
a = (i % 4 >= 2) ? v[i / 4] / 100 : v[i / 4] % 100, v[i] = (i & 1) ? a / 10 : a % 10;
}
}
setsign(1, 1);
}
int get_pos(unsigned pos) const {
return pos >= v.size() ? 0 : v[pos];
}
Int& setsign(int newsign, int rev) {
for (int i = (int) v.size() - 1; i > 0 && v[i] == 0; i--) {
v.erase(v.begin() + i);
}
if (v.size() == 0 || (v.size() == 1 && v[0] == 0)) {
sign = 1;
} else {
sign = rev ? newsign * sign : newsign;
}
return *this;
}
bool absless(const Int& b) const {
if (v.size() != b.v.size()) {
return v.size() < b.v.size();
}
for (int i = (int) v.size() - 1; i >= 0; i--) {
if (v[i] != b.v[i]) {
return v[i] < b.v[i];
}
}
return false;
}
void add_mul(const Int& b, int mul) {
v.resize(std::max(v.size(), b.v.size()) + 2);
for (int i = 0, carry = 0; i < (int) b.v.size() || carry; i++) {
carry += v[i] + b.get_pos(i) * mul;
v[i] = carry % 10000, carry /= 10000;
}
}
std::string to_str() const {
Int b = *this;
std::string s;
for (int i = (b.zip(1), 0); i < (int) b.v.size(); ++i) {
s += char(*(b.v.rbegin() + i) + '0');
}
return (sign < 0 ? "-" : "") + (s.empty() ? std::string("0") : s);
}
public:
Int() : sign(1) {}
Int(const std::string& s) { *this = s; }
Int(int v) {
char buf[21];
sprintf(buf, "%d", v);
*this = buf;
}
Int operator-() const {
Int c = *this;
c.sign = (v.size() > 1 || v[0]) ? -c.sign : 1;
return c;
}
Int& operator=(const std::string& s) {
if (s[0] == '-') {
*this = s.substr(1);
} else {
for (int i = (v.clear(), 0); i < (int) s.size(); ++i) {
v.push_back(*(s.rbegin() + i) - '0');
}
zip(0);
}
return setsign(s[0] == '-' ? -1 : 1, sign = 1);
}
bool operator<(const Int& b) const {
if (sign != b.sign) {
return sign < b.sign;
} else if (sign == 1) {
return absless(b);
} else {
return b.absless(*this);
}
}
bool operator==(const Int& b) const {
return v == b.v && sign == b.sign;
}
Int& operator+=(const Int& b) {
if (sign != b.sign) {
return *this = (*this) - -b;
}
v.resize(std::max(v.size(), b.v.size()) + 1);
for (int i = 0, carry = 0; i < (int) b.v.size() || carry; i++) {
carry += v[i] + b.get_pos(i);
v[i] = carry % 10000, carry /= 10000;
}
return setsign(sign, 0);
}
Int operator+(const Int& b) const {
Int c = *this;
return c += b;
}
Int operator-(const Int& b) const {
if (b.v.empty() || b.v.size() == 1 && b.v[0] == 0) {
return *this;
}
if (sign != b.sign) {
return (*this) + -b;
}
if (absless(b)) {
return -(b - *this);
}
Int c;
for (int i = 0, borrow = 0; i < (int) v.size(); i++) {
borrow += v[i] - b.get_pos(i);
c.v.push_back(borrow);
c.v.back() -= 10000 * (borrow >>= 31);
}
return c.setsign(sign, 0);
}
Int operator*(const Int& b) const {
if (b < *this) {
return b * *this;
}
Int c, d = b;
for (int i = 0; i < (int) v.size(); i++, d.v.insert(d.v.begin(), 0)) {
c.add_mul(d, v[i]);
}
return c.setsign(sign * b.sign, 0);
}
Int operator/(const Int& b) const {
Int c, d;
Int e = b;
e.sign = 1;
d.v.resize(v.size());
double db = 1.0 / (b.v.back() + (b.get_pos((unsigned) b.v.size() - 2) / 1e4) +
(b.get_pos((unsigned) b.v.size() - 3) + 1) / 1e8);
for (int i = (int) v.size() - 1; i >= 0; i--) {
c.v.insert(c.v.begin(), v[i]);
int m = (int) ((c.get_pos((int) e.v.size()) * 10000 + c.get_pos((int) e.v.size() - 1)) * db);
c = c - e * m, c.setsign(c.sign, 0), d.v[i] += m;
while (!(c < e)) {
c = c - e, d.v[i] += 1;
}
}
return d.setsign(sign * b.sign, 0);
}
Int operator%(const Int& b) const { return *this - *this / b * b; }
bool operator>(const Int& b) const { return b < *this; }
bool operator<=(const Int& b) const { return !(b < *this); }
bool operator>=(const Int& b) const { return !(*this < b); }
bool operator!=(const Int& b) const { return !(*this == b); }
friend ostream& operator<<(ostream& os, const Int& a) {
os << a.to_str();
return os;
}
};
/* 用法
Int a, b;
// 赋值
a = 123;
a = "123";
a = std::string("123");
b = a;
// 输出
cout << a << "\n";
cout << a << a << ' ' << a;
// 运算
a = a + b;
a = a - b;
a = a * b;
a = a / b;
// 比较
bool f1 = a < b;
bool f2 = a <= b;
bool f3 = a > b;
bool f4 = a >= b;
bool f5 = a == b;
bool f6 = a != b;
// 参考:https://github.com/Baobaobear/MiniBigInteger/blob/main/bigint_tiny.h
*/
int main() {
int n;
cin >> n;
Int res = 1;
while (n--) {
res = res * 2;
}
cout << res - 1 << "\n";
return 0;
}
2)对于四座塔
思路:
- 首先我们需要明确的一点就是,在满足游戏规则的情况下,将一座塔的所有圆盘移动到另一座塔所需的最少塔数一定是三,我们定义 \(g_j\) 表示在三塔模式下移动 \(j\) 个圆盘的最少移动次数。现在多出来了一座塔。如果不利用这座塔游戏也是可以结束的,但如果利用了一定可以减少移动次数,因此我们重新思考游戏玩法;
- 我们定义 \(f_i\) 表示在三塔模式下移动 \(i\) 个圆盘的最少移动次数,那么游戏玩法一定是:1)首先在四塔模式下将 \(j\ (0\le j\le i-1)\) 个圆盘移动到某一座塔上,2)然后在三塔模式下将剩余 \(i-j\) 个圆盘移动到目标塔上,3)最后将那 j 个圆盘在四塔模式下移动到目标塔上;
- 于是就有状态转移方程:\(f_i = \min{ \{ f_j+g_{i-j}+f_j \} },\ (1\le j\le i-1)\)。
时间复杂度:\(O(n^2)\)
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n = 12;
vector<int> f(n + 1, INT_MAX >> 1);
vector<int> g(n + 1);
for (int j = 0; j <= n; j++) {
g[j] = (1 << j) - 1;
}
f[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++) {
f[i] = min(f[i], f[j] + g[i - j] + f[j]);
}
cout << f[i] << "\n";
}
return 0;
}
同类题推荐:
- CF 1200 * | 反转字符串 | AcWing - (www.acwing.com)
- CF 1300 * | 最大化子数组的总成本 | LeetCode - (leetcode.cn)
- CF 1300 * | 施咒的最大总伤害 | LeetCode - (leetcode.cn)
- CF 1400 * | 费解的开关 | AcWing - (www.acwing.com)
- 洛谷 黄 | 覆盖墙壁 | 洛谷 - (www.luogu.com.cn)
- CF 1800 | Squaring | CF - (codeforces.com)
例:最长上升子序列¶
经典之处:最长上升子序列 (Longest Increasing Subsequence, LIS) 模型
难度:朴素做法约洛谷 橙,优化做法约洛谷 绿
OJ:洛谷
题意:给定长度为 \(n\ (1\le n\le 10^3)\) 的序列 \(a\ (1\le a_i \le 10^6)\),输出其最长上升子序列的长度。
1)思路一:朴素 DP
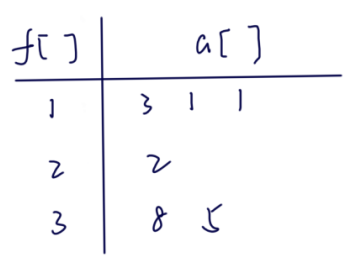
我们定义 \(f_i\) 表示以元素 \(a_i\) 结尾的最长上升子序列的长度,显然初始状态全都是 \(1\)。容易发现,\(f_i\) 需要从 \(a_j < a_i\ (j < i)\) 的状态 \(f_j\) 转移过来,即 \(f_i=\max(f_i,f_j +1)\)。
比如对于下图中 \(i=6\) 的转移情况,其中 ✔ 表示进入了大小判断并转移的逻辑,最终 \(f_i\) 就是从 \(j = 5\) 对应的 \(f_j = 3\) 转移过来得到 \(f_i=4\)。
时间复杂度:\(O(n^2)\)
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<int> f(n, 1);
int ans = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (a[i] > a[j]) {
f[i] = max(f[i], f[j] + 1);
}
}
ans = max(ans, f[i]);
}
cout << ans << "\n";
return 0;
}
2)思路二:贪心 + 二分优化 DP
上述朴素 DP 的核心思路是按位置枚举,这使得状态转移的代价为 \(O(n)\),能不能优化状态转移的代价呢?不妨试着从 \(f\) 的数值大小来枚举,即按前缀的最长上升子序列的长度来枚举。如下图所示:
但这样状态转移的代价仍然是 \(O(n)\) 的。进一步观察可以发现,我们只需要贪心地保留每一个 \(f\) 下最小的元素即可,因为后面的状态肯定是从最小的元素进行转移的,我们将其记作 \(g\) 数组。
并且这样贪心存储后还可以得到一个性质,即 \(f\) 数组中存储的元素一定是严格单调递增的。因为如果不是单调递增,那么更短的长度对应的数值应当更小才对。
有了上述单调的性质后,在求解 \(f_i\) 进行转移时,就可以二分查找右边界找到「比当前元素小 \(g_j < a_i\) 且前缀子序列长度尽可能长 \(\max g_j\)」的位置进行转移了。
时间复杂度:\(O(n \log n)\)
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<int> g(n + 1, INT_MAX >> 1);
g[1] = a[0];
int max_len = 1;
for (int i = 1; i < n; i++) {
// 二分找到比 a[i] 小的最大子序列长度
int l = 0, r = max_len;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (g[mid] < a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
g[r + 1] = min(g[r + 1], a[i]);
// 如果比最大的都长,说明 LIS 的长度可以加 1
max_len += r == max_len;
}
cout << max_len << "\n";
return 0;
}
3)思路三:树状数组优化 DP
TODO
同类题推荐:
例:最长公共子序列¶
经典之处:最长公共子序列 (Longest Common Subsequence, LCS) 模型
难度:洛谷 绿
OJ:洛谷
题意:给定两个长度为 \(n\ (1\le n \le 10^5)\) 的排列 \(a,b\),求其最长公共子序列的长度。
1)常规做法
*注:为了方便,本思路下标从 \(1\) 开始。
思路:定义 \(f_{i,j}\) 表示 \(a\) 序列的前 \(i\) 个元素与 \(b\) 序列的前 \(j\) 个元素的最长公共子序列长度,那么显然有以下状态转移:
- 若 \(a_i\) 与 \(b_j\) 相同,那么 \(f_{i,j}\) 就从 \(f_{i-1,j-1}+1\) 转移过来;
- 若 \(a_i\) 与 \(b_j\) 不同,那么 \(f_{ij}\) 就从 \(f_{i,j-1}\) 和 \(f_{i-1,j}\) 中更大的那个转移过来。
时间复杂度:\(O(n^2)\)
n = int(input().strip())
a = [None] + list(map(int, input().strip().split()))
b = [None] + list(map(int, input().strip().split()))
f = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, n + 1):
if a[i] == b[j]:
f[i][j] = f[i - 1][j - 1] + 1
else:
f[i][j] = max(f[i - 1][j], f[i][j - 1])
print(f[n][n])
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> a(n + 1), b(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
cin >> b[i];
}
vector<vector<int>> f(n + 1, vector<int>(n + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i] == b[j]) {
f[i][j] = f[i - 1][j - 1] + 1;
} else {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
}
}
}
cout << f[n][n] << "\n";
return 0;
}
2)针对本题进行特化
*注:本思路下标从 \(0\) 开始。
思路:
- 本题的数据量显然不适合使用 \(O(n^2)\) 的算法,注意到本题中两个序列都是排列。如果 \(a\) 是单调递增的,那么求解 \(a,b\) 的 LCS 就可以转化为求解 \(b\) 的 LIS 从而使复杂度降至 \(O(n\log n)\);
- 上述转化肯定不能直接用,但是可以学习其转化的思想,即:利用一个序列单调且唯一的属性(上述为数值大小)在另一个序列中寻找该属性的 LIS。我们能不能挖掘出 \(a,b\) 两个排列共有的属性并且让 \(a\) 中该属性单调且唯一呢?有的,就是下标;
- 我们针对 \(a\) 序列建立一个「元素 \(\to\) 下标」的映射表,那么 \(a\) 序列映射到下标后就是单调递增且唯一的,我们只需要求解 \(b\) 序列映射到下标后的 LIS 长度即可。
时间复杂度:\(O(n\log n)\)
def LIS(a: list[int]) -> int:
n = len(a)
g = [10**7] * (n + 1)
max_len = 1
for x in a:
l, r = 0, max_len
while l < r:
mid = (l + r + 1) >> 1
if g[mid] < x:
l = mid
else:
r = mid - 1
g[r + 1] = min(g[r + 1], x)
max_len += r == max_len
return max_len
if __name__ == '__main__':
n = int(input().strip())
arr = list(map(int, input().strip().split()))
f = [0] * (n + 1) # 映射表
for i in range(n):
f[arr[i]] = i
a = [f[x] for x in map(int, input().strip().split())]
print(LIS(a))
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
int LIS(vector<int>& a) {
int n = a.size();
vector<int> g(n + 1, INT_MAX >> 1);
g[1] = a[0];
int max_len = 1;
for (int i = 1; i < n; i++) {
int l = 0, r = max_len;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (g[mid] < a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
g[r + 1] = min(g[r + 1], a[i]);
max_len += r == max_len;
}
return max_len;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> f(n + 1); // 映射表
for (int i = 0; i < n; i++) {
int x;
cin >> x;
f[x] = i;
}
vector<int> a(n);
for (int i = 0; i < n; i++) {
int x;
cin >> x;
a[i] = f[x];
}
cout << LIS(a) << "\n";
return 0;
}
背包 DP¶
例:过河卒¶
https://www.luogu.com.cn/problem/P1002
标签:网格图 dp、dfs
题意:给定一个矩阵,现在需要从左上角走到右下角,问一共有多少种走法?有一个特殊限制是,对于图中的 9 个点是无法通过的。
思路一:dfs
我们可以采用深搜的方法。但是会超时,我们可以这样估算时间复杂度:对于每一个点,我们都需要计算当前点的右下角的矩阵中的每一个点,那么总运算次数就近似为阶乘级别。当然实际的时间复杂度不会这么大,但是这种做法 \(n*m\) 一旦超过 100 就很容易 tle
时间复杂度:\(O(nm!)\)
思路二:dp
我们可以考虑,对于当前的点,可以从哪些点走过来,很显然就是上面一个点和左边一个点,而对于走到当前这个点的路线就是走到上面的点和左边的点的路线之和,base 状态就是
dp[1][1] = 1,即起点的路线数为 1时间复杂度:\(O(nm)\)
dfs 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 30;
int n, m, a, b;
int res;
bool notsafe[N][N];
void init() {
int px[9] = {0, -1, -2, -2, -1, 1, 2, 2, 1};
int py[9] = {0, 2, 1, -1, -2, -2, -1, 1, 2};
for (int i = 0; i < 9; i++) {
int na = a + px[i], nb = b + py[i];
if (na < 0 || nb < 0) continue;
notsafe[na][nb] = true;
}
}
void dfs(int x, int y) {
if (x > n || y > m || notsafe[x][y]) {
return;
}
if (x == n && y == m) {
res++;
return;
}
dfs(x, y + 1);
dfs(x + 1, y);
}
void solve() {
cin >> n >> m >> a >> b;
init();
dfs(0, 0);
cout << res << "\n";
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) solve();
return 0;
}
dp 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 30;
int n, m, a, b;
bool notsafe[N][N];
ll dp[N][N];
void solve() {
cin >> n >> m >> a >> b;
// 初始化
++n, ++m, ++a, ++b;
int px[9] = {0, -1, -2, -2, -1, 1, 2, 2, 1};
int py[9] = {0, 2, 1, -1, -2, -2, -1, 1, 2};
for (int i = 0; i < 9; i++) {
int na = a + px[i], nb = b + py[i];
if (na < 0 || nb < 0) continue;
notsafe[na][nb] = true;
}
// dp求解
dp[1][1] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!notsafe[i - 1][j]) dp[i][j] += dp[i - 1][j];
if (!notsafe[i][j - 1]) dp[i][j] += dp[i][j - 1];
}
}
cout << dp[n][m] << "\n";
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) solve();
return 0;
}
例:摘樱桃 II¶
https://leetcode.cn/problems/cherry-pickup-ii/
题意:给定一个 \(n\) 行 \(m\) 列的网格图,每个格子拥有一个价值。现在有两个人分别从左上角和右上角开始移动,移动方式为「左下、下、右下」三个方向,问两人最终最多一共可以获得多少价值?如果两人同时经过一个位置,则只能算一次价值。
思路:
状态定义。最终状态一定是两人都在最后一行的任意两列,我们如何定义状态可以不重不漏的表示两人的运动状态呢?可以发现两人始终在同一行,但是列数不一定相同,我们定义状态 \(f[i][j][k]\) 表示两人走到第 \(i\) 行时,一人在第 \(j\) 列,另一人在第 \(k\) 列时的总价值。则答案就是:
\[ \max{(f [n-1][j] [k])}, j, k\in [0, m] \]状态转移。本题难点在于状态定义,一旦定义好了以后状态转移就不困难了。对于当前状态 \(f[i][j][k]\),根据乘法原理,两人均有 3 种走法,因此当前状态可以从 \(3\times 3=9\) 种合法状态转移过来。取最大值即可。
时间复杂度:\(O(nm^2)\)
class Solution:
def cherryPickup(self, g: List[List[int]]) -> int:
n, m = len(g), len(g[0])
f = [[[-1] * m for _ in range(m)] for _ in range(n)]
f[0][0][m - 1] = g[0][0] + g[0][m - 1]
for i in range(1, n):
for j in range(m):
for k in range(m):
# 枚举 9 个子问题
for p in range(j - 1, j + 2):
for q in range(k - 1, k + 2):
if 0 <= p < m and 0 <= q < m and f[i - 1][p][q] != -1:
f[i][j][k] = max(f[i][j][k], f[i - 1][p][q] + g[i][j] + (0 if j == k else g[i][k]))
res = 0
for j in range(m):
for k in range(j, m):
res = max(res, f[n - 1][j][k])
return res
例:摘樱桃¶
弱化版 \((n\le 50)\) :https://leetcode.cn/problems/cherry-pickup/
强化版 \((n\le300)\) :https://codeforces.com/problemset/problem/213/C
题意:给定一个 n 行 n 列的网格图,问从左上走到右下,再从右下走到左上最多可以获得多少价值?一个单元格只能被计算一次价值。
注:弱化版中 -1 表示不可达,强化版没有不可达的约束。强化版 AC 代码
思路一:暴力 dp
- 首先对于来回问题可以转化为两次去的问题,即问题等价于求解「两个人从左上角走到右下角」的最大收益。
- 显然我们可以定义四维的状态,其中 \(f[i][j][p][q]\) 表示第一个人走到 \((i,j)\) 且第二个人走到 \((p,q)\) 时的最大收益。直接枚举这四个维度,然后从 4 个合法的子问题转移过来即可。
- 时间复杂度:\(O(n^4)\)
思路二:优化 dp
- 注意到问题可以进一步等价于「两个人 同时 从左上角走到右下角」的最大收益。也就是两个人到起点 \((0,0)\) 的曼哈顿距离应该是一样的,即 \(i+j=p+q\),也就是说如果其中一个人 \((i,j)\) 的位置确定了,则另一个人只需要枚举一个下标,另一个下标就可以 \(O(1)\) 的确定了。可以将时间复杂度降低一个维度。
- 状态定义。我们定义 \(f[k][i_1][i_2]\) 表示第一个人走到 \((i_1,k-i_1)\) 且第二个人走到 \((i_2,k-i_2)\) 时的最大收益。则最终答案就是 \(f[2n-2][n-1][n-1]\)。状态转移同理,从 4 个合法子问题转移过来即可。
- 时间复杂度:\(O(n^3)\)
暴力 dp:
template<class T>
void chmax(T& a, T b) {
a = max(a, b);
}
int di[4] = {-1, -1, 0, 0};
int dj[4] = {0, 0, -1, -1};
int dp[4] = {-1, 0, -1, 0};
int dq[4] = {0, -1, 0, -1};
class Solution {
public:
int cherryPickup(vector<vector<int>>& g) {
int n = g.size();
int f[n][n][n][n];
memset(f, -1, sizeof f);
f[0][0][0][0] = g[0][0] == -1 ? -1 : g[0][0];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (g[i][j] == -1) {
continue;
}
for (int p = 0; p < n; p++) {
for (int q = 0; q < n; q++) {
if (g[p][q] == -1) {
continue;
}
// 枚举 4 个子问题
for (int k = 0; k < 4; k++) {
int ni = i + di[k], nj = j + dj[k];
int np = p + dp[k], nq = q + dq[k];
if (ni >= 0 && nj >= 0 && np >= 0 && nq >= 0 && f[ni][nj][np][nq] != -1) {
chmax(f[i][j][p][q], f[ni][nj][np][nq] + g[i][j] + (i == p && j == q ? 0 : g[p][q]));
}
}
}
}
}
}
return f[n - 1][n - 1][n - 1][n - 1] == -1 ? 0 : f[n - 1][n - 1][n - 1][n - 1];
}
};
优化 dp:
template<class T>
void chmax(T& a, T b) {
a = max(a, b);
}
int dx[] = {0, 0, -1, -1};
int dy[] = {0, -1, 0, -1};
class Solution {
public:
int cherryPickup(vector<vector<int>>& g) {
int n = g.size();
int f[2 * n - 1][n][n];
memset(f, -1, sizeof f);
f[0][0][0] = g[0][0] == -1 ? -1 : g[0][0];
for (int k = 1; k <= 2 * n - 2; k++) {
for (int i1 = 0; i1 < n; i1++) {
for (int i2 = 0; i2 < n; i2++) {
int j1 = k - i1, j2 = k - i2;
if (j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || g[i1][j1] == -1 || g[i2][j2] == -1) {
continue;
}
// 枚举 4 个子问题
for (int t = 0; t < 4; t++) {
int ni1 = i1 + dx[t], nj1 = k - ni1;
int ni2 = i2 + dy[t], nj2 = k - ni2;
if (ni1 >= 0 && nj1 >= 0 && ni2 >= 0 && nj2 >= 0 && f[k - 1][ni1][ni2] != -1) {
chmax(f[k][i1][i2], f[k - 1][ni1][ni2] + g[i1][j1] + (i1 == i2 && j1 == j2 ? 0 : g[i2][j2]));
}
}
}
}
}
return f[2 * n - 2][n - 1][n - 1] == -1 ? 0 : f[2 * n - 2][n - 1][n - 1];
}
};
例:栈¶
https://www.luogu.com.cn/problem/P1044
题意:n 个数依次进栈,随机出栈,问一共有多少种出栈序列?
思路一:dfs
- 我们可以这么构造搜索树:已知对于当前的栈,一共有两种状态
- 入栈 - 如果当前还有数没有入栈
- 出栈 - 如果当前栈内还有元素
- 搜索参数:
i,j表示入栈数为i出栈数为j的状态- 搜索终止条件
- 入栈数 < 出栈数 - \(i<j\)
- 入栈数 > 总数 \(n\) - \(i = n\)
- 答案状态:入栈数为 n,出栈数也为 n
- 时间复杂度:\(O(\text{方案数})\)
思路二:dp
采用上述 dfs 时的状态表示方法,
i,j表示入栈数为i出栈数为j的状态。我们在搜索的时候,考虑的是接下来可以搜索的状态
即出栈一个数的状态 -
i+1,j和入栈一个数的状态 -
i,j+1如图:
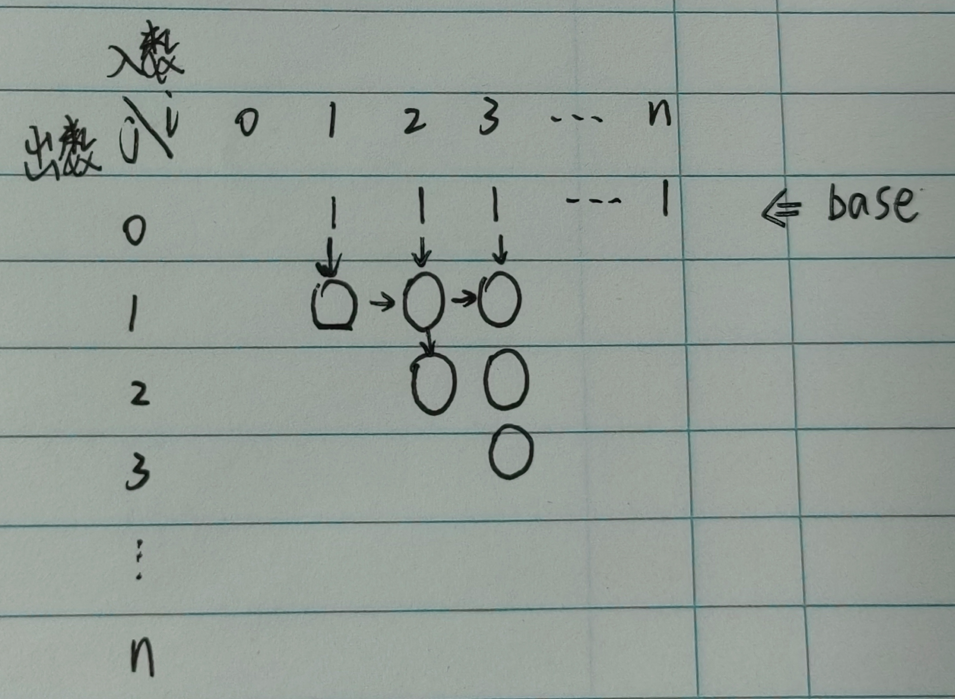
而我们在 dp 的时候,需要考虑的是子结构的解来得出当前状态的答案,就需要考虑之前的状态。即当前状态是从之前的哪些状态转移过来的。和上述 dfs 思路是相反的。我们需要考虑的是
- 上一个状态入栈一个数到当前状态 -
i-1,j\(\to\)i,j上一个状态出栈一个数到当前状态 -
i,j-1\(\to\)i,j特例:\(i=j\) 时,只能是上述第二种状态转移而来,因为要始终保证入栈数大于等于出栈数,即 \(i \ge j\)
如图:
我们知道,入栈数一定是大于等于出栈数的,即 \(i\ge j\)。于是我们在枚举 \(j\) 的时候,枚举的范围是 \([1,i]\)
\(base\) 状态的构建取决于 \(j=0\) 时的所有状态,我们知道没有任何数出栈也是一种状态,于是
\[ dp [i][0] = 0,(i = 1,2,3,..., n) \]时间复杂度:\(O(n^2)\)
dfs 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, res;
// 入栈i个数,出栈j个数
void dfs(int i, int j) {
if (i < j || i > n) return;
if (i == n && j == n) res++;
dfs(i + 1, j);
dfs(i, j + 1);
}
void solve() {
cin >> n;
dfs(0, 0);
cout << res << "\n";
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) solve();
return 0;
}
dp 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 20;
int n;
ll dp[N][N]; // dp[i][j] 表示入栈数为i,出栈数为j的方案总数
void solve() {
cin >> n;
// base状态:没有数出栈也是一种状态
for (int i = 1; i <= n; i++) dp[i][0] = 1;
// dp转移
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
if (i == j) dp[i][j] = dp[i][j - 1];
else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
cout << dp[n][n] << "\n";
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) solve();
return 0;
}
例:找出稳定的二进制数组 II¶
https://leetcode.cn/problems/find-all-possible-stable-binary-arrays-ii/
题意:构造一个仅含有 \(n\) 个 \(0\),\(m\) 个 \(1\) 的数组,且长度超过 \(k\) 的子数组必须同时含有 \(0\) 和 \(1\)。给出构造的总方案数对 \(10^9+7\) 取余后的结果。
思路:
定义状态表。我们从左到右确定每一位的数字时,需要确定这么三个信息:当前是哪一位?还剩几个 \(0\) 和 \(1\)?这一位填 \(0\) 还是 \(1\)?对于这三个信息,我们可以定义状态数组 \(f[i][j][k]\) 表示当前已经选了 \(i\) 个 \(0\),\(j\) 个 \(1\),且第 \(i+j\) 位填 \(k\) 时的方案数。这样最终答案就是 \(f[n][m][0]+f[n][m][1]\)。
定义子问题。以当前第 \(i+j\) 位填 \(0\) 为例,填 \(1\) 同理,即当前需要维护的是 \(f[i][j][0]\)。显然的如果前一位是和当前位不同,即 \(1\) 时,可以直接转移过来;如果前一位和当前位相同,即 \(0\) 时,有可能会出现长度超过 \(k\) 的连续 \(0\) 子数组,即前段数组刚好是以「一个 \(1\) 和 \(k\) 个 \(0\) 结尾的」合法数组,此时再拼接一个 \(0\) 就不合法了。
状态转移方程。综上所述,可以得到以下两个状态转移方程:
\[ \begin{aligned} f [i][j] [0] = f [i - 1][j] [1] + f [i - 1][j] [0] - f [i - k - 1][j] [1] \\ f [i][j] [1] = f [i][j - 1] [0] + f [i][j - 1] [1] - f [i][j - k - 1] [0] \end{aligned} \]时间复杂度:\(O(nm)\)
class Solution {
public:
int numberOfStableArrays(int n, int m, int k) {
const int mod = 1e9 + 7;
vector<vector<array<int, 2>>> f(n + 1, vector<array<int, 2>>(m + 1));
for (int i = 0; i <= min(n, k); i++) {
f[i][0][0] = 1;
}
for (int j = 0; j <= min(m, k); j++) {
f[0][j][1] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
f[i][j][0] = (f[i - 1][j][1] + f[i - 1][j][0]) % mod;
if (i - k - 1 >= 0) {
f[i][j][0] = (f[i][j][0] - f[i - k - 1][j][1] + mod) % mod;
}
f[i][j][1] = (f[i][j - 1][0] + f[i][j - 1][1]) % mod;
if (j - k - 1 >= 0) {
f[i][j][1] = (f[i][j][1] - f[i][j - k - 1][0] + mod) % mod;
}
}
}
return (f[n][m][0] + f[n][m][1]) % mod;
}
};
例:学生出勤记录 II¶
https://leetcode.cn/problems/student-attendance-record-ii/description/
题意:构造一个仅含有 \(P,A,L\) 三种字符的字符串,使得 \(A\) 最多出现 \(1\) 次,同时 \(L\) 最多连续出现 \(2\) 次。问一共有多少种构造方案?对 \(10^9+7\) 取模。
思路:
- 模拟分析问题。我们从前往后构造。对于当前第 \(i\) 个字符 \(s[i]\),有 \(3\) 种可能的选项,其中 \(P\) 是一定合法的选项,\(A\) 是否合法取决于 \(s[0:i-1]\) 中的 \(A\) 的数量,\(L\) 是否合法取决于 \(s[0:i-1]\) 的末尾连续 \(L\) 的数量。因此我们可以通过 被动转移 的动态规划求解。
- 状态定义。从上述分析不难发现需要 \(3\) 种状态来表示所有情况,因此我们定义 \(f[i][j][k]\) 表示构造第 \(i\) 位时,\(s[0:i]\) 中含有 \(j\) 个 \(A\) 且末尾含有连续 \(k\) 个 \(L\) 时的方案数。
- 初始化。每一位填什么取决于前缀 \(s[0:i-1]\) 的情况,因此我们需要初始化 \(f[0][][]\) 即第 \(0\) 位的情况。显然的第 \(0\) 位 \(P,A,L\) 三种都可以填,对应的就是 \(f[0][0][0] = f[0][1][0] = f[0][0][1] = 1\),其余初始化为 \(0\) 即可。
- 状态转移。考虑第 \(i\) 位的三种情况:
- 填 \(P\):可以用前缀的所有状态来更新 \(f[i][j][0]\)
- 填 \(A\):可以用前缀中不含 \(A\) 的所有状态来更新 \(f[i][1][0]\)
- 填 \(L\):可以用前缀中末尾不超过 \(1\) 位 \(L\) 的所有状态来更新 \(f[i][j][k]\)
- 最终答案。为 \(\displaystyle \sum_{j=0}^{1}\sum_{k=0}^{2}f[n-1][j][k]\)。
时间复杂度:\(\Theta (6n)\)
class Solution {
public:
int checkRecord(int n) {
const int mod = 1e9 + 7;
// f[i][j][k]表示从左往右构造第i位时,s[0:i]中含有j个A且尾部含有连续k个L时的方案数
int f[n][2][3];
memset(f, 0, sizeof f);
// 初始化
f[0][0][0] = f[0][1][0] = f[0][0][1] = 1;
// 转移
for (int i = 1; i < n; i++) {
// s[i]填P
for (int j = 0; j <= 1; j++) {
for (int k = 0; k <= 2; k++) {
f[i][j][0] = (f[i][j][0] + f[i - 1][j][k]) % mod;
}
}
// s[i]填A
for (int k = 0; k <= 2; k++) {
f[i][1][0] = (f[i][1][0] + f[i - 1][0][k]) % mod;
}
// s[i]填L
for (int j = 0; j <= 1; j++) {
for (int k = 1; k <= 2; k++) {
f[i][j][k] = (f[i][j][k] + f[i - 1][j][k - 1]) % mod;
}
}
}
// 计算答案
int res = 0;
for (int j = 0; j <= 1; j++) {
for (int k = 0; k <= 2; k++) {
res = (res + f[n - 1][j][k]) % mod;
}
}
return res;
}
};
class Solution:
def checkRecord(self, n: int) -> int:
mod = int(1e9 + 7)
f = [[[0, 0, 0] for _ in range(2)] for _ in range(n)]
f[0][0][0] = f[0][1][0] = f[0][0][1] = 1
for i in range(1, n):
# P
for j in range(2):
for k in range(3):
f[i][j][0] = (f[i][j][0] + f[i - 1][j][k]) % mod
# A
for k in range(3):
f[i][1][0] = (f[i][1][0] + f[i - 1][0][k]) % mod
# L
for j in range(2):
for k in range(1, 3):
f[i][j][k] = (f[i][j][k] + f[i - 1][j][k - 1]) % mod
res = 0
for j in range(2):
for k in range(3):
res = (res + f[n - 1][j][k]) % mod
return res
区间 DP¶
例:对称山脉¶
https://www.acwing.com/problem/content/5169/
模拟,时间复杂度 \(O(n^3)\)
#include <iostream>
#include <cmath>
using namespace std;
const int N = 5010;
int n;
int a[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
// 枚举区间长度
for (int len = 1; len <= n; len++) {
int res = 2e9;
// 枚举相应长度的所有区间
for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
// 计算区间的不对称值
int l = i, r = j;
int sum = 0;
while (l < r) {
sum += abs(a[l] - a[r]);
l++, r--;
}
res = min(res, sum);
}
cout << res << ' ';
}
return 0;
}
dp 优化,时间复杂度 \(O(n^2)\)
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
const int N = 5010;
int n;
int a[N];
int dp[N][N]; // dp[i][j] 表示第 i 到 j 的不对称值
int res[N]; // res[len] 表示长度为 len 的山脉的最小不对称值
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
memset(res, 0x3f, sizeof res);
// 长度为 1 的情况
res[1] = 0;
// 长度为 2 的情况
for (int i = 1, j = i + 1; j <= n; i++, j++) {
dp[i][j] = abs(a[i] - a[j]);
res[2] = min(res[2], dp[i][j]);
}
// 长度 >= 3 的情况
for (int len = 3; len <= n; len++) {
for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
dp[i][j] = dp[i + 1][j - 1] + abs(a[i] - a[j]);
res[len] = min(res[len], dp[i][j]);
}
}
for (int i = 1; i <= n; i++)
cout << res[i] << ' ';
return 0;
}
数位 DP¶
树形 DP¶
例:最大社交深度和¶
https://vijos.org/d/nnu_contest/p/1534
算法:树形 dp、BFS
题意:给定一棵树,现在需要选择其中的一个结点为根节点,使得深度和最大。深度的定义是以每个结点到树根所经历的结点数
思路一:暴力
显然可以直接遍历每一个结点,计算每个结点的深度和,然后取最大值即可
时间复杂度:\(O(n^2)\)
思路二:树形 dp
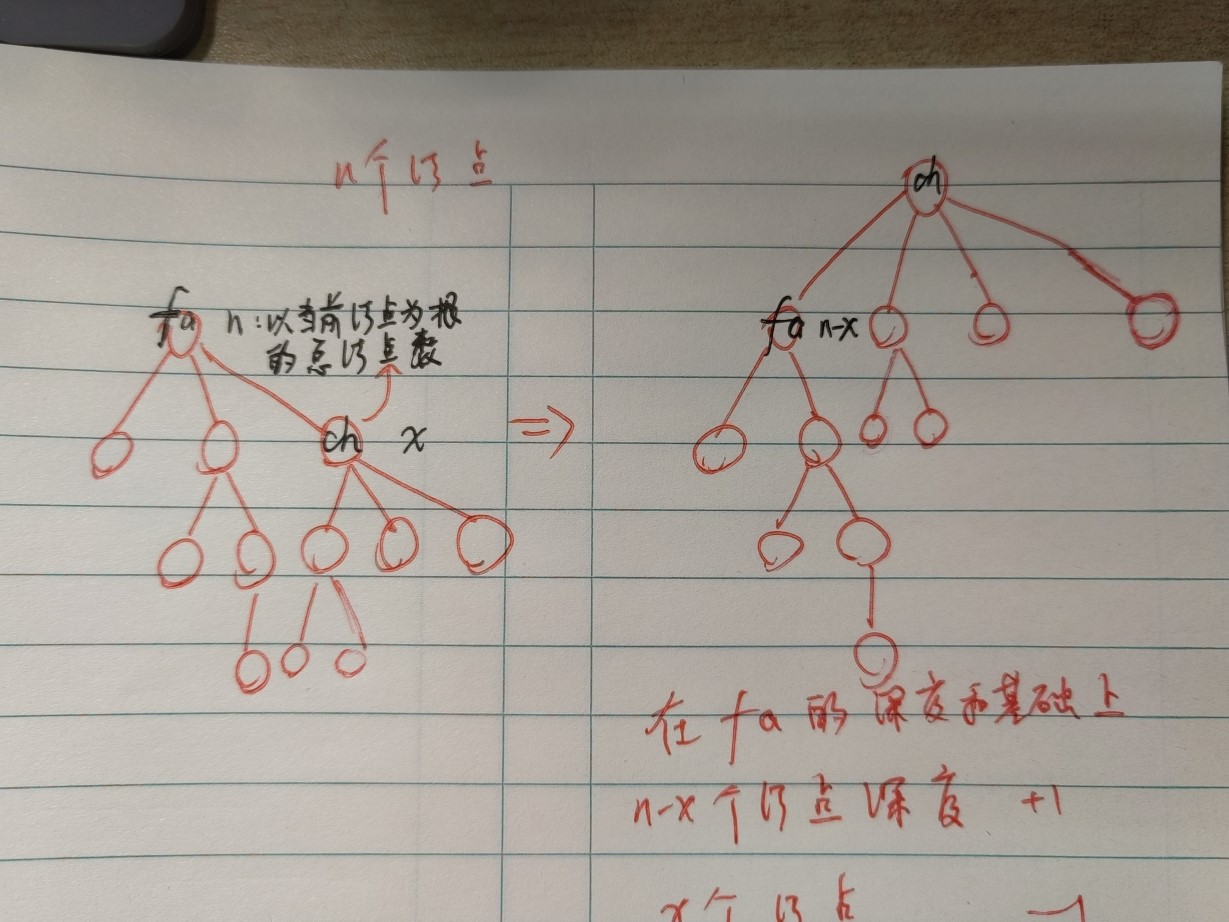
我们可以发现,对于当前的根结点
fa,我们选择其中的一个子结点ch,将ch作为新的根结点(如右图)。那么对于当前的ch的深度和,我们可以借助fa的深度和进行求解。我们假设以ch为子树的结点总数为x,那么这x个结点在换根之后,相对于ch的深度和,贡献了-x的深度;而对于fa的剩下来的n-x个结点,相对于ch的深度和,贡献了n-x的深度。于是ch的深度和就是fa的深度和-x+n-x,即:\[ dep [ch] = dep [fa]-x+n-x = dep [fa]+n-2\times x \]于是我们很快就能想到利用前后层的递推关系,\(O(1)\) 的计算出所有子结点的深度和。
代码实现:我们可以先计算出
base的情况,即任选一个结点作为根结点,然后基于此进行迭代计算。在迭代计算的时候需要注意的点就是在一遍dfs计算某个结点的深度和dep[root]时,如果希望同时计算出每一个结点作为子树时,子树的结点数,显然需要分治计算一波。关于分治的计算我熟练度不够高,~~特此标注一下 debug 了 3h 的点~~:即在递归到最底层,进行回溯计算的时候,需要注意不能统计父结点的结点值(因为建的是双向图,所以一定会有从父结点回溯的情况),那么为了避开这个点,就需要在 \(O(1)\) 的时间复杂度内获得当前结点的父结点的编号,从而进行特判,采用的方式就是增加递归参数fa。没有考虑从父结点回溯的情况的 dfs 代码
考虑了从父结点回溯的情况的 dfs 代码
时间复杂度:\(O(n)\)
暴力代码:
const int N = 500010;
int n;
vector<int> G[N];
int st[N], dep[N];
void dfs(int id, int now, int depth) {
if (!st[now]) {
st[now] = 1;
dep[id] += depth;
for (auto& node: G[now]) {
dfs(id, node, depth + 1);
}
}
}
void solve() {
cin >> n;
for (int i = 1; i <= n - 1; i++) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
int res = 0;
for (int i = 1; i <= n; i++) {
memset(st, 0, sizeof st);
dfs(i, i, 1);
res = max(res, dep[i]);
}
cout << res << "\n";
}
优化代码:
const int N = 500010;
int n, dep[N], root = 1;
vector<int> G[N], cnt(N, 1);;
bool st[N];
// 当前结点编号 now,当前结点的父结点 fa,当前结点深度 depth
void dfs(int now, int fa, int depth) {
if (!st[now]) {
st[now] = true;
dep[root] += depth;
for (auto& ch: G[now]) {
dfs(ch, now, depth + 1);
if (ch != fa) {
cnt[now] += cnt[ch];
}
}
}
}
void bfs() {
memset(st, 0, sizeof st);
queue<int> q;
q.push(root);
st[root] = true;
while (q.size()) {
int fa = q.front(); // 父结点编号 fa
q.pop();
for (auto& ch: G[fa]) {
if (!st[ch]) {
st[ch] = true;
dep[ch] = dep[fa] + n - 2 * cnt[ch];
q.push(ch);
}
}
}
}
void solve() {
cin >> n;
for (int i = 1; i <= n - 1; i++) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
dfs(root, -1, 1);
bfs();
cout << *max_element(dep, dep + n + 1) << "\n";
}
状压 DP¶
例:Avoid K Palindrome¶
https://atcoder.jp/contests/abc359/tasks/abc359_d
题意:给定一个长度为 \(n\le 1000\) 的字符串 \(s\) 和一个整数 \(k\le10\),其中含有若干个
'A','B'和'?'。其中'?'可以转化为'A'或'B',假设有 \(q\) 和'?',则一共可以转化出 \(2^q\) 个不同的 \(s\)。问所有转化出的 \(s\) 中,有多少是不含有长度为 \(k\) 的回文子串的。思路:最暴力的做法就是 2^q 枚举所有可能的字符串,然后再 O(n) 的检查,这样时间复杂度为 \(O(n2^n)\),只能通过 20 以内的数据。一般字符串回文问题可以考虑 dp。
例:吃奶酪¶
https://www.luogu.com.cn/problem/P1433
题意:给定一个平面直角坐标系与 n 个点的坐标,起点在坐标原点。问如何选择行进路线使得到达每一个点且总路程最短
思路一:爆搜。题中的 \(n \le 15\) 直接无脑爆搜,但是 TLE。爆搜的思路为:每次选择其中的一个点,接下来选择剩余的没有被选择过的点继续搜索,知道所有的点全部都搜到为止
时间复杂度:\(O(n!)\)
思路二:状态压缩 DP。
时间复杂度:\(O()\)
爆搜代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 20;
int n;
double res = 4000.0;
bool vis[N];
struct Idx {
double x, y;
} a[N];
double d(Idx be, Idx en) {
return sqrt((be.x - en.x) * (be.x - en.x) + (be.y - en.y) * (be.y - en.y));
}
// 父结点坐标 fa,当前结点次序 now,当前路径长度 len
void dfs(Idx fa, int now, double len) {
vis[now] = true;
if (count(vis + 1, vis + n + 1, true) == n) {
res = min(res, len);
}
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(a[now], i, len + d(a[now], a[i]));
vis[now] = false;
}
void solve() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y;
}
for (int i = 1; i <= n; i++) {
Idx fa = {0, 0};
dfs(fa, i, d(fa, a[i]));
}
cout << fixed << setprecision(2) << res << "\n";
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) solve();
return 0;
}
状压 dp 代码
概率 DP¶
TODO
计数 DP¶
TODO