基础算法

基础因人而异，下面罗列的是个人认为相对基础的知识点。只有熟练掌握了以下基础算法，才有可能理解更复杂的算法从而解出更高难度的问题。

一些做题小技巧：

贪心：善用枚举，可以从一两个元素开始考虑；
前缀和与差分：遇到区间修改操作时，应该立即想到其等价于对差分数组做端点修改操作；
二分：当按照题意进行正面模拟发现难以实现或者复杂度过高时，可以观察变量之间是否有单调性关系；
递归：搜索类题目，脑子里始终有一个搜索树，无论是具象化的树的题，还是可以抽象为树的搜索题；分治类题目，思考能不能先解决子问题，然后利用解决好的所有子问题来解决当前局面的问题。

贪心

贪心考虑的是局部最优，即每次做决策时都是选当前的局部最优解。当然，如果能举出贪心的反例，即局部最优无法得出全局最优，就可以考虑使用动态规划等其他全局性策略来解决问题了。

贪心算法其实并不简单，很多时候需要敢想敢猜并且证明并不容易，但因为这种方法套路不多，就放在第一个基础算法部分展开。对于贪心问题的证明，我总结出了以下证明方法：

交换法：如果交换两个对象会得到更差的结果，那么原来的方案（顺序）就是合理的；
边界法：由于边界也需要满足相同的条件，并且边界的情况往往更少，因此从边界开始考虑（枚举）往往可以证明出贪心的正确性。也可以理解为从更小规模的问题开始考虑。

例：ABBC or BACB

经典之处：翻转操作 $\xrightarrow{\text{看作}}$ 平移操作

难度：CF 1500

OJ：CF

题意：现在有一个由 A 和 B 两种字符组成的字符串 $s\ (1\le|s|\le2\cdot 10^5)$。操作一，可以将 AB 转化为 BC；操作二，可以将 BA 转化为 CB。问最多可以执行上述操作多少次。

思路：

容易发现，题意中的两种翻转操作可以转化为平移操作。即，两种操作都可以看做是对 B 字符的移动，操作一是向左移动，操作二是向右移动。于是题目就转化为了怎么选择每一个 B 字符的移动方向可以尽可能多的经过 A 字符；
不难发现，如果字符串的边缘有 B 字符或者有至少两个连续的 B 字符，那么所有的 A 字符都能被经过。反之，就是单独的 B 字符将一个完整的 A 串切割开来的情景，此时就是小学学到的线段模型，选择长度最短的 A 子串不经过即可。

时间复杂度：$O(n)$

PythonC++

T = int(input())
for _ in range(T):
    s = input()
    cnt_A = s.count('A')
    if s[0] == 'B' or s[-1] == 'B' or s.count('BB'):
        print(cnt_A)
    else:
        min_len_A = len(s)  # 最短 A 串长度
        i = 0
        while i < len(s):
            if s[i] == 'A':
                j = i
                while j < len(s) and s[j] == 'A':
                    j += 1
                min_len_A = min(min_len_A, j - i)
                i = j
            else:
                i += 1
        print(cnt_A - min_len_A)

#include <algorithm>
#include <climits>
#include <iostream>
using namespace std;

void solve() {
    string s;
    cin >> s;

    int cnt_A = count(s.begin(), s.end(), 'A');

    auto check_bb = [](string& s) -> bool {
        for (int i = 1; i < s.size(); i++) {
            if (s[i] == s[i - 1] && s[i] == 'B') {
                return true;
            }
        }
        return false;
    };

    if (s[0] == 'B' || s[s.size() - 1] == 'B' || check_bb(s)) {
        cout << cnt_A << "\n";
        return;
    }

    int min_len_A = INT_MAX / 2;  // 最短 A 串长度
    for (int i = 0; i < s.size(); ) {
        if (s[i] == 'A') {
            int j = i;
            while (j < s.size() && s[j] == 'A') {
                j++;
            }
            min_len_A = min(min_len_A, j - i);
            i = j + 1;
        } else {
            i++;
        }
    }
    cout << cnt_A - min_len_A << "\n";
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

同类题推荐：

CF 1300 * | 力扣 | 修改后的最大二进制字符串 - (leetcode.cn)

例：子序列最大优雅度

经典之处：反悔贪心

难度：CF 1800 *

OJ：力扣

题意：给定长度为 $n \ (1\le n \le 10^5)$ 的二元组序列，二元组表示每一个元素的价值与种类。现在需要从中寻找一个长度为 $k$ 的子序列使得该序列「所有物品价值之和 + 物品种类数的平方」的值最大。返回该最大值。

思路：我们采用反悔贪心的思路。首先按照物品本身价值进行降序排序并选择前 $k$ 个物品作为集合 $S$，然后按顺序枚举剩下的物品进行替换决策。当且仅当集合 S 有物品的类别重复且剩下物品的类别不存在于集合 $S$ 中才有可能让答案更大。

时间复杂度：$O(n \log n)$

PythonC++

class Solution:
    def findMaximumElegance(self, items: List[List[int]], k: int) -> int:
        n = len(items)
        items.sort(key=lambda x: -x[0])

        # 贪心
        val, cat = 0, 0
        cnt = [0] * (n + 1)
        rep = []
        for i in range(k):
            v, c = items[i]
            val += v
            cat += cnt[c] == 0
            cnt[c] += 1
            if cnt[c] > 1:
                rep.append(v)

        # 反悔
        ans = val + cat ** 2
        for i in range(k, n):
            v, c = items[i]
            if cnt[c] == 0 and len(rep):
                val -= rep.pop()
                val += v
                cat += 1
                cnt[c] += 1
                ans = max(ans, val + cat ** 2)

        return ans

using ll = long long;

class Solution {
public:
    ll findMaximumElegance(vector<vector<int>>& items, int k) {
        int n = items.size();
        sort(items.rbegin(), items.rend());

        // 贪心
        ll val = 0, cat = 0;
        vector<int> cnt(n + 1, 0);
        vector<int> rep;
        for (int i = 0; i < k; i++) {
            int v = items[i][0], c = items[i][1];
            val += v;
            cat += !cnt[c];
            cnt[c] += 1;
            if (cnt[c] > 1) {
                rep.push_back(v);
            }
        }

        // 反悔
        ll ans = val + cat * cat;
        for (int i = k; i < n; i++) {
            int v = items[i][0], c = items[i][1];
            if (!cnt[c] && !rep.empty()) {
                val += v;
                val -= rep.back();
                rep.pop_back();
                cnt[c] += 1;
                cat += 1;
                ans = max(ans, val + cat * cat);
            }
        }

        return ans;
    }
};

同类题推荐：

原料采购 | 第 16 届蓝桥杯 Python A 组最后一题

例：起床困难综合症

经典之处：按位贪心

难度：洛谷绿

OJ：洛谷

题意：给定 $n\ (2 \le n \le 10^5)$ 个操作对，每个操作对包含一个位运算（「按位与、按位或、按位异或」三者之一）和一个操作数 $t\ (0 \le t \le 10^9)$。现在需要选择一个初始值 $num\in{\{0, 1, \cdots,m\}},\ (2 \le m \le 10^9)$，使得 $num$ 经过这 $n$ 次二元运算后得到的结果最大。输出最大运算结果。

思路：

由于三种操作是相邻无关的，因此我们可以按每一个二进制位单独考虑。对于第 $i$ 位，初始值为 $0$ 或 $1$ 在经过 $n$ 次运算后均有可能得到 $0$ 和 $1$，因此我们有 $4$ 种情况需要讨论，每种情况贪心地选择最优即可；
而为了让结果最大，我们需要从高位开始枚举。因为当初始值填 $1$ 更优时，如果先填低位，可能会导致高位填不了 $1$ 从而得不到最大的答案值。

时间复杂度：$O(n)$

PythonC++

n, m = map(int, input().strip().split())

x, y = 0, -1
for _ in range(n):
    inp = input().strip().split()
    op, t = inp[0], int(inp[1])
    if op == "AND":
        x &= t
        y &= t
    elif op == "OR":
        x |= t
        y |= t
    else:
        x ^= t
        y ^= t

ans, num = 0, 0
for i in range(30, -1, -1):
    a, b = (x >> i) & 1, (y >> i) & 1
    # 下列四种情况可以简化，为了逻辑清晰性就不简化了
    if a and b:
        ans |= 1 << i
    elif a and not b:
        ans |= 1 << i
    elif not a and b:
        if num | (1 << i) <= m:
            num |= 1 << i
            ans |= 1 << i
    else:
        pass

print(ans)

#include <iostream>
#include <vector>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    vector<pair<string, int>> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i].first >> a[i].second;
    }

    // 预处理所有可能的结果
    int x = 0, y = -1;
    for (int i = 0; i < n; i++) {
        auto [op, t] = a[i];
        if (op == "AND") {
            x &= t;
            y &= t;
        } else if (op == "OR") {
            x |= t;
            y |= t;
        } else {
            x ^= t;
            y ^= t;
        }
    }

    // 从高位开始贪心选择
    int ans = 0, num = 0;
    for (int i = 30; i >= 0; i--) {
        int a = (x >> i) & 1, b = (y >> i) & 1;
        if (a == 1 && b == 0) {
            ans |= 1 << i;
        } else if (a == 0 && b == 1 && ((num | (1 << i)) <= m)) {
            num |= 1 << i;
            ans |= 1 << i;
        } else if (a == 1 && b == 1) {
            ans |= 1 << i;
        }
    }

    cout << ans << "\n";

    return 0;
}

前缀和与差分

前缀和与差分是两个相辅相成的算法。两者的适用场景如下：

前缀和算法适用于「频繁求子数组之和、不频繁修改数组元素」的场景；
差分算法适用于「频繁增减子数组元素值、不频繁求数组元素」的场景。

更精简地说：

前缀和算法适用于「频繁区间查询、不频繁单点修改」的场景；
差分算法适用于「频繁区间修改、不频繁单点查询」的场景。

前缀和

为了学习差分算法，我们有必要先学习前缀和算法。具体地，对于一个长度为 $n$ 的数组 $a$，我们定义 $s_i$ 表示：

\[ s_i =\sum_{j = 0}^{i}a_j \]

那么当进行区间查询求解数组中下标在闭区间 $[p,q]$ 中的元素和时，只需要 $s_q-s_{p-1}$ 地 $O(1)$ 计算出来即可。我们称 $s$ 为数组 $a$ 的前缀和数组。为了维护出 $s$，我们采用递推策略。即：

\[ s_i = \begin{cases} a_0,&i = 0\\ s_{i-1}+a_i,&i\ge1 \end{cases} \]

差分

为了实现给数组中下标在闭区间 $[i,j]$ 中的元素 $s_{i\sim j}$ 同时增加 $x$ 的操作，我们可以借助前缀和算法的思想。具体地，仍然记原始数组为 $a$，前缀和数组为 $s$，如果将 $a_i+x$ 同时 $a_{j+1}-x$，那么在维护前缀和数组 $s$ 时，$s_{i\sim j}$ 中的每一个元素就都增加了 $x$ 且 $s$ 中的其他元素值保持不变。

利用上述思路，我们可以将待操作的数组看做已经维护好的前缀和数组 $s$，并利用 $a_i=s_i-s_{i-1}$ 维护出数组 $a$，后续如果需要频繁地给待操作数组 $s$ 进行区间修改，只需要 $O(1)$ 地修改 $a$ 数组的两个边界即可。这里的 $a$ 数组就叫做差分数组，这种修改思想就被称为差分算法。

综上所述：

前缀和算法高效的前提是数组元素尽可能保持不变。如果需要频繁地变动数组元素，利用前缀和算法进行区间求和就不合适了；
差分算法高效的前提是不需要频繁地索引数组元素，如果需要频繁地索引数组元素，利用差分算法进行区间修改也就不合适了。

Tip

如果需要同时频繁地「区间修改、区间查询」，可以使用进阶数据结构诸如树状数组或线段树来实现。

例：Decode

经典之处：看到 01 数量相等，试着将 $0$ 转成 $-1$ 用前缀和做

难度：CF 1600

OJ：CF

题意：给定一个 01 字符串 $s\ (1\le \lvert s \rvert \le 2\cdot10^5)$，计算 $s$ 的所有子区间中 01 数量相等的子串数量，将结果对 $10^9+7$ 取模。

思路：

下标从 $1$ 开始，采用枚举右维护左的策略来枚举所有合法子串。即统计「以 $s_i\ (i\in [1,n])$ 结尾的合法子串」在所有区间中的数量，最朴素的做法就是利用前缀和，枚举 $j \in [0,i-1]$ 并统计区间长度是区间和两倍的子串数量，但这是 $O(n^2)$ 的，无法通过本题；
引入 01 串的前缀和维护 trick：当 s[i] == '0' 时，将其记作 -1，当 s[i] == '1' 时，仍然记作 1。这样我们就可以将「枚举 $j$ 寻找合法区间个数」的操作转化为「统计 pre[j] == pre[i] 个数」的操作，而这显然可以通过哈希表/桶/红黑树来维护，从而将枚举 $j$ 的时间复杂度从 $O(n)$ 降至 $O(1)$ 或 $O(\log n)$；
容易发现，一个合法的 $j$ 对应的子串 $s_{j+1\sim i}$ 存在于 $(j+1)\cdot (n-i+1)$ 个区间中，也就意味着对最终答案也贡献了这么多，因此我们在枚举 $i$ 时只需要统计所有合法的 $j$ 即可，而这在上一步就已经完成了。

时间复杂度：$O(n)$

PythonC++

from collections import defaultdict

T = int(input().strip())
OUTs = []
for _ in range(T):
    s = input().strip()
    n = len(s)

    pre = [0] * (n + 1)
    for i in range(n):
        pre[i + 1] = pre[i] + (-1 if s[i] == '0' else 1)

    ans = 0
    cnt = defaultdict(int)
    cnt[0] = 1
    for i in range(1, n + 1):
        ans = (ans + cnt[pre[i]] * (n - i + 1)) % (10**9 + 7)
        cnt[pre[i]] += i + 1

    OUTs.append(ans)

print('\n'.join(map(str, OUTs)))

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
using ll = long long;

const int MOD = 1e9 + 7;

void solve() {
    string s;
    cin >> s;

    int n = s.size();
    vector<int> pre(n + 1);
    for (int i = 0; i < n; i++) {
        pre[i + 1] = pre[i] + (s[i] == '0' ? -1 : 1);
    }

    int ans = 0;
    unordered_map<int, ll> cnt;
    cnt[0] = 1;
    for (int i = 1; i <= n; i++) {
        ans = (1ll * ans + cnt[pre[i]] * (n - i + 1)) % MOD;
        cnt[pre[i]] += i + 1;
    }

    cout << ans << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

同类题推荐：

CF 1300 * | 截断数组 | AcWing - (www.acwing.com)

例：铺设道路

经典之处：区间修改 $\xrightarrow{\text{差分}}$ 单点修改。

难度：洛谷黄

OJ：洛谷

题意：给定一个含有 $n\ (1 \le n \le 10^5)$ 个数序列 $a\ (0\le a_i\le 10^4)$，每次操作可以让一个区间内所有数减一，前提是区间中的数都要 $\ge1$。输出将所有的数全部都减到 $0$ 的最小操作次数。

思路：看到区间操作，首先想到差分。于是区间操作就等价于修改差分数组 b，那么区间的最小操作次数就等价于 b[l]--, b[r+1]++ 的最小操作次数。由于 b[r+1]++ 不是必须的（因为右端点不一定需要存在，即给序列的整个右半段执行区间操作），因此本题的答案就是 $\sum_{i=0}^{n-1}b_i\cdot \mathbb I(b_i>0)$。

时间复杂度：$O(n)$

PythonC++

n = int(input())
a = list(map(int, input().split()))

ans = a[0]
for i in range(1, n):
    ans += max(0, a[i] - a[i - 1])

print(ans)

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    int ans = 0;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        if (!i) {
            ans += a[i];
        } else {
            ans += max(0, a[i] - a[i - 1]);
        }
    }

    cout << ans << "\n";

    return 0;
}

同类题推荐：

CF 1500 * | 增减序列 | AcWing - (www.acwing.com)

二分

二分本质上是对「单调序列」进行加速查询的操作。按照不同思考问题的角度，二分算法又分为二分查找与二分答案，其中二分查找可以理解为由因及果，而二分答案可以理解为由果追因。

二分查找

如果你会按照字母的顺序查字典，那么你一定可以立刻理解二分查找算法。一般地，假设有一个含有 $n$ 个元素的序列 $a$，其属性 $attr$ 是单调递增的。现在想要查询属性 $attr$ 取值为 $tar$ 的元素在序列中的位置 $idx$。显然我们可以遍历一边序列 $a$ 得到结果，但由于属性 $attr$ 是单调的，在下标范围为 $[l,r]$ 的序列中查找时，只需要不断比较 $a_{(l+r)/2}$ 和 $tar$ 的值即可，具体地：

如果 $a_{(l+r)/2}>tar$，那么 $idx$ 一定在 $[l,(l+r)/2]$ 中；
如果 $a_{(l+r)/2}<tar$，那么 $idx$ 一定在 $[(l+r)/2,r]$ 中；
如果 $a_{(l+r)/2}=tar$，那么 $idx$ 就是 $(l+r)/2$。

这类题目一般都可以归纳为：给定自变量 $x$，问在满足某个约束的情况下，$x$ 的最值是多少。假定 x 的值域为 $[low,high]$，那么这里的 $x$ 在 $[low,lim]$ 时是满足（不满足）约束的，在 $[lim,high]$ 是不满足（满足）约束的。这种性质也被称为「二段性」，具备了这种性质，我们直接在 $x$ 的值域中二分查找 $lim$ 即可。

二分答案

二分答案其实就是二分查找，只不过你需要敏锐地发现需要「待求解的答案」与「满足约束的状态」满足上文提到的二段性，仅此而已。

例：木材加工

经典之处：二分答案找右边界模板

难度：洛谷黄

OJ：洛谷

题意：给定 $n\ (1\le n \le 10^5)$ 根木头，现在需要将这些木头切成 $k\ (1\le k \le 10^8)$ 段等长的小段，问小段的最大长度是多少。

思路：小段长度越长，可切出的小段就越少，具备单调性，那么直接二分小段长度，找到最大的小段长度值使得可切出的小段个数 $\ge k$ 即可。

时间复杂度：$O(n\log k)$

PythonC++

n, k = map(int, input().strip().split())
a = [int(input()) for _ in range(n)]

def chk(v: int) -> bool:
    s = 0
    for x in a:
        s += x // v
    return s >= k

l, r = 0, max(a)
while l < r:
    mid = (l + r + 1) >> 1
    if chk(mid):
        l = mid
    else:
        r = mid - 1

print(l)

#include <iostream>
#include <vector>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    ll n, k;
    cin >> n >> k;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    auto chk = [&](int v) -> bool {
        ll cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt += a[i] / v;
        }
        return cnt >= k;
    };

    int l = 0, r = 1e8;
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (chk(mid)) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }

    cout << r << "\n";

    return 0;
}

例：盖楼

经典之处：二分答案找左边界模板、集合的思维

难度：CF 1400 *

OJ：AcWing

题意：给定 $n,m,x,y\ (1\le n,m\le10^9,2\le x,y< 30000)$，其中 $x$ 和 $y$ 均为质数。现在有一个排列数数组，需要将数组中的部分数字分配给两个人。其中一个人需要 $n$ 个数且不允许给它能被 $x$ 整除的数，另一个人需要 $m$ 个数且不允许给它能被 $y$ 整除的数。问这个排列数数组的大小最小是多少。

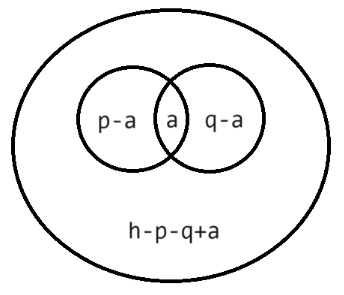
思路：假设排列数共有 $h$ 个，能被 $x$ 整除的数有 $p$ 个，能被 $y$ 整除的数有 $q$ 个，能同时被 $x$ 和 $y$ 整除的数有 $a$ 个。一种贪心的分配策略就是，优先将自己不要的数分配给对方，然后再从 $h-p-q+a$ 中分配。由于 $h$ 越大，可分配的数字就越多，为了找到最小的 $h$，套二分查找左边界的板子即可。

时间复杂度：$O(\log n)$

PythonC++

n, m, x, y = map(int, input().strip().split())

def chk(h: int) -> bool:
    p = h // x
    q = h // y
    a = h // (x * y)
    return h - p - q + a < max(0, n - (q - a)) + max(0, m - (p - a))

l, r = 0, 10**15
while l < r:
    mid = (l + r) >> 1
    if chk(mid):
        l = mid + 1
    else:
        r = mid

print(l)

#include <iostream>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m, x, y;
    cin >> n >> m >> x >> y;

    auto chk = [&](ll h) -> bool {
        ll p = h / x, q = h / y, a = h / (x * y);
        return h - p - q + a < max(0ll, n - (q - a)) + max(0ll, m - (p - a));
    };

    ll l = 1, r = 1e15;
    while (l < r) {
        ll mid = (l + r) >> 1;
        if (chk(mid)) {
            l = mid + 1;
        } else {
            r = mid;
        }
    }

    cout << r << "\n";

    return 0;
}

同类题推荐：

递归

递归是编程入门的最后一关，也是打开新世界的钥匙。所谓递归，就是让一个函数自己调用自己从而实现一系列诸如：搜索、分治、回溯等算法。

关于递归函数中调用自己的操作，你可以先不用 care 她到底是怎么执行的，你只需要关心她到底做了什么。比如现在有一个需求，需要封装一个函数 sum(x) 返回 $\sum_{i=1}^x,\ (x\ge 1)$ 的计算结果。你完全可以写出下面的程序：

int sum(int x) {
    int ans = 0;
    for (int i = 1; i <= x; i++) {
        ans += i;
    }
    return ans;
}

但如果使用递归，就可以不用 for 循环，比如下面的程序：

int sum(int x) {
    if (x == 1) {
        return 1;
    }
    return x + sum(x - 1);
}

你不需要关心 sum(x - 1) 到底发生了什么，你只需要知道她算出了 $\sum_{i=1}^{x-1}$，那么再加上 $x$ 就是 $\sum_{i=1}^x$，是不是很简单？

当然，你一定发现了第三行的 return 语句，这是为了让函数递归调用自己时有一个终点。所有的递归函数都有一个终点，如果递归的终点是可控的，就可以不写 return 语句（比如在遍历图时），但上述程序的终点显然是不可控的，因为程序并不知道什么时候不需要再调用 sum(x - 1)。

推而广之，所有使用递归思想的算法都有同一套逻辑：

return_type function_name(param) {
    // 1. 递归终点处理逻辑
    // 2. 当前状态处理逻辑
    // 3. 调用自己解决逻辑一致但规模更小的子问题
}

现在可以学习使用递归逻辑的一系列算法了。

搜索

所谓搜索，就是在一个「解空间」中通过递归程序将所有可行解搜索出来的算法。这里的解空间可能有些抽象，我们就以一棵根树（可以简单查阅一下树的定义）为例。假设一个问题的解空间就是一棵根树（无环连通图，后用树代称），答案就存在树中的某些结点上。那么我们要做的就是遍历这棵树从而找到所有的可行解。

那么问题来了，怎么遍历？我们知道树有着很多优美的性质，比如以任意一个结点为根都对应了一棵和根树完全一样的结构，而这恰好满足前文所说的「逻辑完全一样但是规模更小」的递归性质。因此遍历一棵树只需要两个逻辑：

遍历当前结点；
遍历当前结点的所有子结点。

而这，就可以称作搜索。以上述树的搜索为例，就有下面的伪代码：

return_type search(int node_index) {
    // 1. 处理当前结点
    // 2. 遍历所有子结点
}

没有返回值？确实。如果我们单纯的遍历一棵树，是不需要返回值的，因为当前结点的所有子结点都遍历结束后，程序就会开始回溯。相比于上面的 sum(x) 函数，这里的递归终点是已经存在的。

分治

分治是一个很有意思的递归算法，其在上述搜索算法基础之上更进一步。分治算法的核心思想是将原问题转化为多个互不重叠（互斥）的子问题，通过优先求解子问题，来加速原问题的求解 ¹。

分治算法可以总结为以下三个步骤：

divide：将原问题问题划分为多个互不重叠的子问题；
conquer：递归处理子问题；
combine：联合子问题的处理结果加速计算原问题的求解。

当然，如果一个问题无法拆分为多个互斥的子问题，分治算法就不适用了，此时可以采用更高效的动态规划算法来尝试解决。

快速排序。这是一种不稳定的排序算法（如果一个排序算法在对所有元素排序后，原来相同关键字的顺序保持不变，则称该排序算法是稳定的，反之就是不稳定的），核心思想就是分治。具体地，以升序为例，如果一个序列是有序的，那么对于该序列中的每一个元素，其左边所有元素都应该比右边所有元素小。基于该先验，我们就有了快速排序算法：

选择序列中任意一个元素作为基准；
基于该基准，扫描一遍序列将比基准小的元素排在基准的左边，比基准大的元素排在基准的右边；
递归左右两边的序列直到序列只有 1 个元素为止。

在计算时间复杂度时，我们可以将分治的逻辑想象成一棵二叉树，对于二叉树的每一层都会有 $O(n)$ 的遍历开销，而二叉树的层数平均有 $O(\log n)$ 层，因此排序的时间复杂度就是 $O(n\log n)$。当然如果每次选择的基准刚好是所在序列的最值，就会导致二叉树的层数退化到 $O(n)$，但一般来说不会这么极端。

C++ 示例代码

vector<int> a = {3, 1, 4, 2, 5};  // 待排序数组

void quick_sort(int l, int r) {
    if (l >= r) return;

    // conquer
    int i = l - 1, j = r + 1, x = a[(l + r) >> 1];
    while (i < j) {
        while (a[++i] < x);
        while (a[--j] > x);
        if (i < j) swap(a[i], a[j]);
    }

    // divide
    quick_sort(l, j);
    quick_sort(j + 1, r);
}

quick_sort(0, a.size() - 1);  // 调用示例

归并排序。这是一种稳定的排序算法，核心思想同样是分治且符合标准的三步分治策略。同样以升序为例，如果两个有序序列都是升序或都是降序，那么可以双指针扫描一遍从而 $O(n)$ 地合并这两个序列为一个有序序列。基于该先验，我们就有了归并排序算法：

将序列等分为左右两部分；
分治左右两部分使得左右两部分都是升序或都是降序；
合并左右两个有序序列。

时间复杂度的计算与快速排序类似，只不过这里的分治递归二叉树一定是 $O(\log n)$ 层，那么时间复杂度就是稳定的 $O(n \log n)$。

C++ 示例代码

vector<int> a = {3, 1, 4, 2, 5};  // 待排序数组
vector<int> t(a.size(), 0);       // 临时数组

void merge_sort(int l, int r) {
    if (l >= r) return;

    // divide
    int mid = (l + r) >> 1;

    // conquer
    merge_sort(l, mid), merge_sort(mid + 1, r);

    // combine
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (a[i] < a[j]) t[k++] = a[i++];
        else t[k++] = a[j++];
        cnt++;
    }
    while (i <= mid) t[k++] = a[i++];
    while (j <= r) t[k++] = a[j++];

    for (i = l, j = 0; i <= r; i++) a[i] = t[j++];
};

merge_sort(0, a.size() - 1);  // 调用示例

回溯

回溯算法在上述分治的基础之上更进一步。其实按理来说，递归函数的出栈就是回溯，但是这里介绍的回溯更多侧重于递归函数回溯后返回给当前问题的结果。举个例子，我们看看校长是怎么惩罚翘课学生的：从最高的校长开始，ta 不 care 你上没上课，ta 只需要向各个学院的院长询问情况即可，而各个院长也不 care 你上没上课，ta 们只需要向所有年级的辅导员询问情况即可，而辅导员也不 care 你上没上课，ta 们只需要向所有的任课老师询问情况即可，任课老师上课点名了，你没来？那你有福了，任课老师和辅导员说你没来上课，辅导员和院长说你没来上课，院长和校长说你没来上课，校长知道了，那你彻底凉了（才怪）。

至此一个现实场景中的回溯策略就淋漓尽致地体现出来了。通过将原问题划分为多个不重叠的子问题，按照相同逻辑处理完子问题后，原问题得到了所有子问题的解，基于这些子问题的解就可以得到原问题的解，这就是回溯的思想。

总结一下。聪明的你一定发现了，搜索、分治和回溯是层层递进的。搜索是正向试探的勇士，不断的寻找可能的结果，分治是懂得偷懒的领导，通过合理分配工作达到最佳办事效率，而回溯则是顾全大局的谋士，基于所有的已知结果做出最终的选择。

例：组合总和

经典之处：组合型枚举

难度：CF 1200 *

OJ：力扣

题意：给定一个含有 $n\ (1\le n \le 30)$ 个不重复元素的序列，问如何选取其中的元素（可重复选），能够使得选出的数字总和为 $\text{target}\ (1\le \text{target}\le 40)$。给出所有具体选数方案（不考虑数字的选择顺序）。

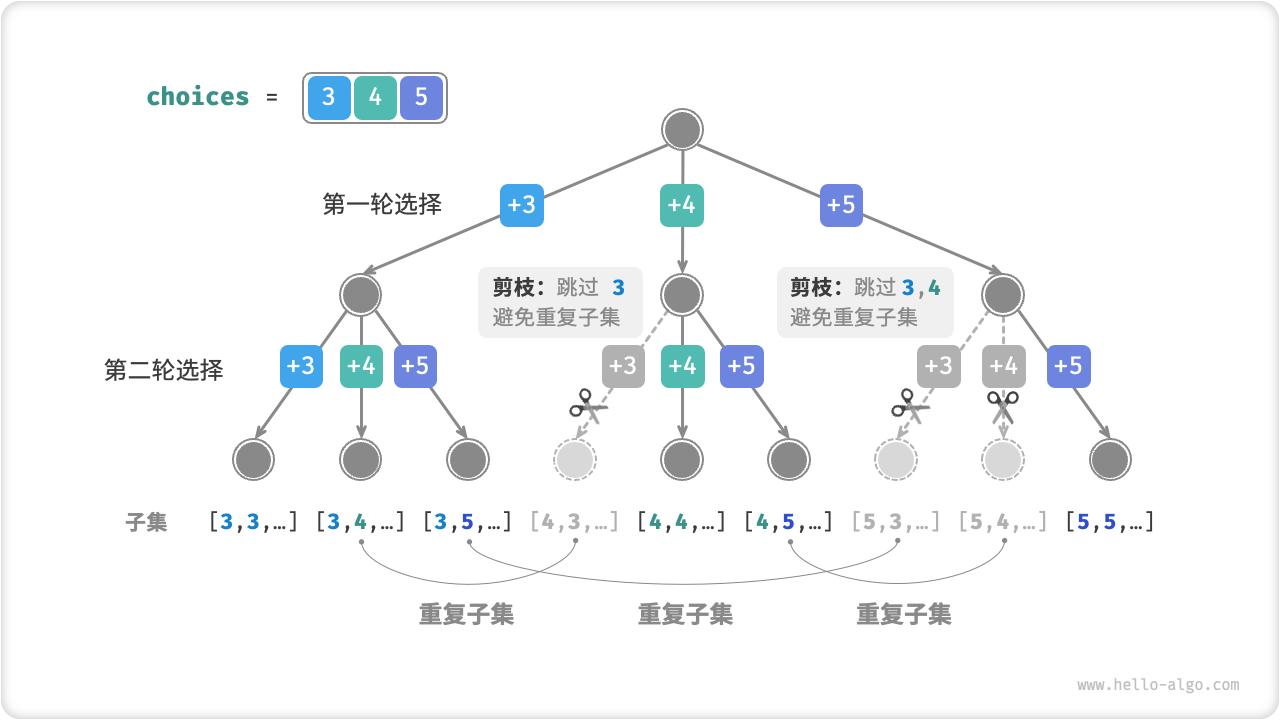
思路：不考虑顺序就是组合数，即组合型搜索经典例题。在枚举序列中的元素时，需要从上一次枚举结束的位置开始，防止方案重复（也可以理解为剪枝操作）。下图对组合型搜索进行了可视化：

时间复杂度：不太会计算时间复杂度，但是在本题的数据量下通过剪枝可以很快的算出方案。具体复杂度推导见三种方法：选或不选/枚举选哪个/完全背包预处理+可行性剪枝 | 灵茶山艾府 - (leetcode.cn)。

PythonC++

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        n = len(candidates)
        ans = []
        path = []

        def dfs(remain: int, idx: int) -> None:
            if remain < 0:
                return
            elif remain == 0:
                ans.append(path.copy())  # 对于列表，append 的是一个引用，所以要加 copy
                return
            for i in range(idx, n):
                path.append(candidates[i])
                dfs(remain - candidates[i], i)
                path.pop()

        dfs(target, 0)

        return ans

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        int n = candidates.size();
        vector<vector<int>> ans;
        vector<int> path;

        function<void(int, int)> dfs = [&](int remain, int idx) {
            if (remain < 0) {
                return;
            } else if (remain == 0) {
                ans.push_back(path);
                return;
            }
            for (int i = idx; i < n; i++) {
                path.push_back(candidates[i]);
                dfs(remain - candidates[i], i);
                path.pop_back();
            }
        };

        dfs(target, 0);

        return ans;
    }
};

例：石头分散的最少移动次数

经典之处：排列型枚举

难度： CF 1400 *

OJ：力扣

题意：给定一个 $3\times 3$ 的矩阵 $g$，其中数字总和为 $9$ 且 $g[i][j] \ge 0$，现在需要将其中 $>1$ 的数字沿着直角边移动到值为 $0$ 的位置上使得最终矩阵全为 $1$，输出最小的总移动距离。

思路：

记 $0$ 为空位，假设有 $k$ 个空位，那么就一定有 $k$ 个 $1$ 可以移动，因此这道题本质上就是 $k$ 个空位与 $k$ 个 $1$ 的匹配问题。为了不漏掉任何一种匹配方式，我们直接全排列枚举空位或者 $1$ 的位置即可，此处我们选择前者；
Python 和 C++ 都内置了全排列的库函数：
- C++ 的全排列枚举库函数为 std::next_permutation(ItFirst, ItEnd)，每次返回刚好比当前排列字典序大的排列；
- Python 的全排列枚举库函数为 itertools.permutations(Iterable)，按照字典序一次性返回所有排列。

时间复杂度：$O(9\times 9!)$

PythonPython 库函数C++C++ 库函数

class Solution:
    def minimumMoves(self, g: List[List[int]]) -> int:
        a = []  # 存 0 的位置
        b = []  # 存 1 的位置
        for i in range(3):
            for j in range(3):
                if g[i][j] == 0:
                    a.append((i, j))
                elif g[i][j] > 1:
                    b.extend([(i, j)] * (g[i][j] - 1))

        ans = 1000
        n = len(a)
        vis = [False] * n

        def dfs(i: int, now: int) -> None:
            if i == n:
                nonlocal ans
                ans = min(ans, now)
                return

            # i 是 1，j 是空位
            for j in range(n):
                if vis[j]:
                    continue
                vis[j] = True
                dfs(
                    i + 1,
                    now + abs(a[j][0] - b[i][0]) + abs(a[j][1] - b[i][1])
                )
                vis[j] = False

        dfs(0, 0)

        return ans

from itertools import permutations

class Solution:
    def minimumMoves(self, g: List[List[int]]) -> int:
        a = []
        b = []
        for i in range(3):
            for j in range(3):
                if g[i][j] == 0:
                    a.append((i, j))
                elif g[i][j] > 1:
                    for _ in range(g[i][j] - 1):
                        b.append((i, j))

        ans = 1000
        for p in permutations(a):
            now = 0
            for i, (x, y) in enumerate(p):
                now += abs(x - b[i][0]) + abs(y - b[i][1])
            ans = min(ans, now)

        return ans

class Solution {
public:
    int minimumMoves(vector<vector<int>>& g) {
        vector<array<int, 2>> a, b;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (g[i][j] == 0) {
                    a.push_back({i, j});
                } else if (g[i][j] > 1) {
                    for (int _ = 0; _ < g[i][j] - 1; _++) {
                        b.push_back({i, j});
                    }
                }
            }
        }

        int ans = 1000;
        int n = a.size();
        vector<bool> vis(n);

        auto dfs = [&](auto&& dfs, int i, int now) -> void {
            if (i == n) {
                ans = min(ans, now);
                return;
            }
            for (int j = 0; j < n; j++) {
                if (vis[j]) {
                    continue;
                }
                vis[j] = true;
                dfs(
                    dfs,
                    i + 1,
                    now + abs(a[j][0] - b[i][0]) + abs(a[j][1] - b[i][1])
                );
                vis[j] = false;
            }
        };

        dfs(dfs, 0, 0);

        return ans;
    }
};

class Solution {
public:
    int minimumMoves(vector<vector<int>>& g) {
        vector<array<int, 2>> a, b;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (g[i][j] == 0) {
                    a.push_back({i, j});
                } else if (g[i][j] > 1) {
                    for (int _ = 0; _ < g[i][j] - 1; _++) {
                        b.push_back({i, j});
                    }
                }
            }
        }

        int ans = 1000;
        do {
            int now = 0;
            for (int i = 0; i < a.size(); i++) {
                now += abs(a[i][0] - b[i][0]) + abs(a[i][1] - b[i][1]);
            }
            ans = min(ans, now);
        } while (next_permutation(a.begin(), a.end()));

        return ans;
    }
};

例：扩展字符串

经典之处：预处理设置上限 trick

难度：CF 1500 *

OJ：AcWing

题意：给定一种字符串构造方法，进行 $q\ (1\le q\le 10)$ 次查询，每次询问第 $n\ (0\le n\le 10^5)$ 个字符串中第 $k\ (1\le k \le 10^{18})$ 个字符是什么（字符串下标从 $1$ 开始）。如果越界输出 '.'。字符串构造方法如下：

$s_0 = $ DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB；
$s_i = $ DKER EPH VOS GOLNJ UKLMH QHNGLNJ A $+s_{i−1}+$ AB CPH VOS FSQVB DLMM VOS QHNG A $+s_{i−1}+$ AB。

思路：

可以发现字符串构造方法类似二叉递归的形式，我们预处理每一个状态的字符串长度后直接递归搜索即可；
由于 $n$ 的上限很大，直接存储每一个状态的长度肯定会炸（C++ 炸 long long，Python 会因为高精炸时空）。注意到询问的下标索引不超过 $10^{18}$，因此我们在预处理时给每一个状态的字符串长度设置上限即可。

时间复杂度：$O(qn)$

PythonC++

import sys
sys.setrecursionlimit(100000)

s = "DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB"
t0 = "DKER EPH VOS GOLNJ UKLMH QHNGLNJ A"
t1 = "AB CPH VOS FSQVB DLMM VOS QHNG A"
t2 = "AB"
l0, l1, l2 = len(t0), len(t1), len(t2)

a = [0] * 100001
a[0] = len(s)
for i in range(1, 100001):
    a[i] = min(2 * 10**18, l0 + l1 + l2 + a[i - 1] * 2)

def dfs(n: int, k: int) -> str:
    if k > a[n]:
        return '.'
    if n == 0:
        return s[k - 1]

    if k > l0 + a[n - 1] + l1 + a[n - 1]:
        return t2[k - (l0 + a[n - 1] + l1 + a[n - 1]) - 1]
    elif k > l0 + a[n - 1] + l1:
        return dfs(n - 1, k - (l0 + a[n - 1] + l1))
    elif k > l0 + a[n - 1]:
        return t1[k - (l0 + a[n - 1]) - 1]
    elif k > l0:
        return dfs(n - 1, k - l0)

    return t0[k - 1]

q = int(input())
ans = ''
for _ in range(q):
    n, k = map(int, input().strip().split())
    ans += dfs(n, k)

print(ans)

#include <iostream>
#include <vector>

using namespace std;
using ll = long long;

const int N = 100001;

ll a[N];
string s = "DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB";
string t0 = "DKER EPH VOS GOLNJ UKLMH QHNGLNJ A";
string t1 = "AB CPH VOS FSQVB DLMM VOS QHNG A";
string t2 = "AB";
int l0 = t0.size();
int l1 = t1.size();
int l2 = t2.size();

char dfs(int n, ll k) {
    if (k > a[n]) {
        return '.';
    }
    if (n == 0) {
        return s[k - 1];
    }

    if (k > l0 + a[n - 1] + l1 + a[n - 1]) {
        return t2[k - (l0 + a[n - 1] + l1 + a[n - 1]) - 1];
    } else if (k > l0 + a[n - 1] + l1) {
        return dfs(n - 1, k - (l0 + a[n - 1] + l1));
    } else if (k > l0 + a[n - 1]) {
        return t1[k - (l0 + a[n - 1]) - 1];
    } else if (k > l0) {
        return dfs(n - 1, k - l0);
    } else {
        return t0[k - 1];
    }
}

int main() {
    a[0] = s.size();
    for (int i = 1; i < N; i++) {
        a[i] = min((ll)2E18, l0 + l1 + l2 + a[i - 1] * 2);
    }

    int q;
    cin >> q;

    string ans = "";
    while (q--) {
        int n;
        ll k;
        cin >> n >> k;
        ans += dfs(n, k);
    }

    cout << ans << "\n";

    return 0;
}

例：01 迷宫

经典之处：连通分量板子题

难度：洛谷黄

OJ：洛谷

题意：给定一个 $n\times n\ (1\le n\le 1000)$ 的 01 方阵，询问 $m\ (1\le m\le 10^5)$ 次，每次询问从 $i,j\ (1\le i,j\le n)$ 出发可以移动多少格。移动规则为：可以走到曼哈顿距离为 $1$ 且与当前数值不同的四个格子中。

思路：

一道入门级网格图遍历问题，放在这主要是为了熟悉连通分量的概念以及 DFS、BFS 和 DSU 在这类问题上的板子写法；
回到本题，显然不可能问一次遍历一次，考虑预处理。预处理就直接遍历网格图同时标记每一个连通分量的大小即可。这里有一个遍历的小 trick，在遍历时保留走过的路径，遍历结束后给走过的路径全都赋上连通分量的大小即可，即二次遍历；
本题也可以用并查集实现，通过给每一个结点添加一个「大小域」来维护每一个结点所在连通分量的结点个数，相较于上述二次遍历策略，时间上的常数会小一点。

时间复杂度：$O(n^2)$

Python BFSPython DSUC++ DFS

from collections import deque

n, m = map(int, input().strip().split())
g = [""] * n
for i in range(n):
    g[i] = input().strip()

ans = [[0] * n for _ in range(n)]
vis = [[False] * n for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

def bfs(i: int, j: int) -> None:
    cnt = 0
    path = []
    q = deque()

    cnt += 1
    path.append((i, j))
    vis[i][j] = True
    q.append((i, j))
    while q:
        x, y = q.popleft()
        for k in range(4):
            nx, ny = dx[k] + x, dy[k] + y
            if nx < 0 or nx >= n or ny < 0 or ny >= n:
                continue
            if vis[nx][ny] or int(g[x][y]) ^ int(g[nx][ny]) == 0:
                continue
            cnt += 1
            path.append((nx, ny))
            vis[nx][ny] = True
            q.append((nx, ny))

    for x, y in path:
        ans[x][y] = cnt

for i in range(n):
    for j in range(n):
        if not vis[i][j]:
            bfs(i, j)

for _ in range(m):
    i, j = map(int, input().strip().split())
    print(ans[i - 1][j - 1])

from collections import deque

class DSU:
    def __init__(self, n: int) -> None:
        self.n = n
        self.sz = n
        self.p = [i for i in range(n)]
        self.cnt = [1 for i in range(n)]

    def find(self, x: int) -> int:
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def merge(self, a: int, b: int) -> None:
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            self.p[pa] = pb
            self.cnt[pb] += self.cnt[pa]
            self.sz -= 1

    def same(self, a: int, b: int) -> bool:
        return self.find(a) == self.find(b)

    def size(self) -> int:
        return self.sz

    def size(self, a: int) -> int:
        return self.cnt[self.find(a)]

n, m = map(int, input().strip().split())
g = [""] * n
for i in range(n):
    g[i] = input().strip()

dsu = DSU(n * n)
vis = [[False] * n for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

def bfs(i: int, j: int) -> None:
    q = deque()
    vis[i][j] = True
    q.append((i, j))

    while q:
        x, y = q.popleft()
        for k in range(4):
            nx, ny = dx[k] + x, dy[k] + y
            if nx < 0 or nx >= n or ny < 0 or ny >= n:
                continue
            if vis[nx][ny] or int(g[x][y]) ^ int(g[nx][ny]) == 0:
                continue

            dsu.merge(x * n + y, nx * n + ny)

            vis[nx][ny] = True
            q.append((nx, ny))

for i in range(n):
    for j in range(n):
        if not vis[i][j]:
            bfs(i, j)

for _ in range(m):
    i, j = map(int, input().strip().split())
    i -= 1
    j -= 1
    print(dsu.size(i * n + j))

#include <iostream>
#include <vector>

using namespace std;

const int N = 1010;

int n, m;
string g[N];
int ans[N][N];
bool vis[N][N];

int cnt;
vector<pair<int, int>> path;
int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};

void dfs(int i, int j) {
    path.push_back({i, j});
    vis[i][j] = true;
    cnt += 1;
    for (int k = 0; k < 4; k++) {
        int nx = i + dx[k], ny = j + dy[k];
        if (nx < 0 || nx >= n || ny < 0 || ny >= n || 
            vis[nx][ny] || (g[nx][ny] - '0') ^ (g[i][j] - '0') == 0) {
            continue;
        }
        dfs(nx, ny);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> g[i];
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (vis[i][j]) {
                continue;
            }
            cnt = 0;
            path.clear();
            dfs(i, j);
            for (auto& [x, y]: path) {
                ans[x][y] = cnt;
            }
        }
    }

    while (m--) {
        int i, j;
        cin >> i >> j;
        cout << ans[i - 1][j - 1] << "\n";
    }

    return 0;
}

同类题推荐：

登山 | 第 16 届蓝桥杯 Python A 组倒数第二题

例：随机排列

经典之处：分治法求解逆序数板子题

难度：CF 1400 *

OJ：AcWing

题意：现在将一个含有 $n\ (2\le n\le 10^6)$ 个数的自然排列（即升序序列）进行 $3n$ 次或 $7n+1$ 次的对换操作，问是对换了 $3n$ 次还是 $7n+1$ 次，若是前者输出 $1$，后者输出 $2$。

思路：

一看到排列对换，立刻想到一个结论：在排列中进行一次对换操作，排列的逆序数的奇偶性就会发生一次变化；
容易发现 $3n \equiv n \pmod 2,7n+1 \equiv n+1 \pmod 2$，因此两种对换次数下，排列的逆序数的奇偶性是不一样的，这就可以成为区分两种对换次数的判别依据。即若 $n$ 为偶数，则对换 $3n$ 次后排列的逆序数一定是偶数，对换 $7n+1$ 次后排列的逆序数一定是奇数，反之同理；
发现了上述性质后，本题就变成了求序列逆序数的板子题。可以借助归并排序的分治思想求解。

时间复杂度：$O(n \log n)$

PythonC++

n = int(input().strip())
a = list(map(int, input().strip().split()))

def merge_sort(l: int, r: int) -> int:
    if l >= r:
        return 0

    # divide
    mid = (l + r) >> 1

    # conquer
    ans = merge_sort(l, mid) + merge_sort(mid + 1, r)

    # combine
    t = []
    i, j = l, mid + 1
    while i <= mid and j <= r:
        if a[i] <= a[j]:
            t.append(a[i])
            i += 1
        else:
            t.append(a[j])
            j += 1
            ans += mid - i + 1  # 点睛之笔
    while i <= mid:
        t.append(a[i])
        i += 1
    while j <= r:
        t.append(a[j])
        j += 1
    a[l:r+1] = t

    return ans

cnt = merge_sort(0, n - 1)

if n & 1:
    print(1 if cnt & 1 else 2)
else:
    print(2 if cnt & 1 else 1)

#include <iostream>
#include <vector>

using namespace std;
using ll = long long;

const int N = 1000010;

int n;
int a[N];

ll merge_sort(int l, int r) {
    if (l >= r) {
        return 0;
    }

    // divide
    int mid = (l + r) >> 1;

    // conquer
    ll ans = merge_sort(l, mid) + merge_sort(mid + 1, r);

    // combine
    int i = l, j = mid + 1;
    vector<int> t;
    while (i <= mid && j <= r) {
        if (a[i] <= a[j]) {
            t.push_back(a[i++]);
        } else {
            t.push_back(a[j++]);
            ans += mid - i + 1;  // 点睛之笔
        }
    }
    while (i <= mid) {
        t.push_back(a[i++]);
    }
    while (j <= r) {
        t.push_back(a[j++]);
    }
    for (int k = l, idx = 0; k <= r; k++) {
        a[k] = t[idx++];
    }

    return ans;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    ll cnt = merge_sort(0, n - 1);

    if (n & 1) {
        cout << (cnt & 1 ? 1 : 2) << "\n";
    } else {
        cout << (cnt & 1 ? 2 : 1) << "\n";
    }

    return 0;
}

Divide-and-conquer algorithm | WIKIPEDIA - (en.wikipedia.org) ↩