跳转至

线性搜索

本章介绍最优化问题中迭代解 \(x_{k+1} = x_k + \alpha_kd_k\) 基于「线性搜索」的迭代方式。

假设搜索方向 \(d_{k}\) 是一个定值且一定是下降方向，我们讨论步长因子 \(\alpha_{k}\) 的计算选择策略。分为两步：

  1. 确定步长的搜索区间
  2. 通过精确 or 不精确算法来搜索合适的步长

本章的内容分布：

  • 3.1 介绍 确定初始搜索区间 的「进退法」
  • 3.2 介绍 缩小搜索区间 的「精确线性搜索算法」：0.618 法、斐波那契法、二分法、插值法
  • 3.3 介绍 缩小搜索区间 的「不精确线性搜索算法」：Armijo 准则、Goldstein 准则、Wolfe 准则

确定初始搜索区间

确定初始搜索区间 \([a,b]\)，我们利用 进退法

精确线性搜索算法

预备知识：单峰函数定理

在正式开始介绍之前，我们先了解 单峰函数定理：

  • 定理：对于在区间 \([a,b]\) 上的一个单峰函数 \(f(x)\)，\(x^* \in [a,b]\) 是其极小点，\(x_1\) 和 \(x_2\) 是 \([a,b]\) 上的任意两点，且 \(a<x_1<x_2<b\)，可以通过比较 \(f(x_1),f(x_2)\) 的值来确定点的保留和舍弃

  • 迭代：

    1. 若 \(f(x_1) \ge f(x_2)\) 则 \(x^* \in [x_1,b]\)

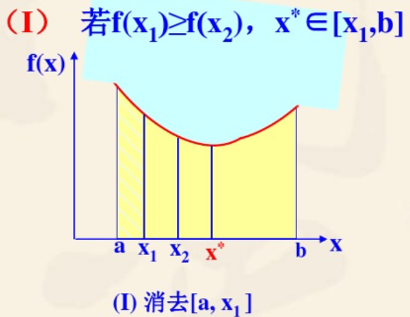
      保留右区间

    2. 若 \(f(x_1) < f(x_2)\) 则 \(x^* \in [a,x_2]\)​

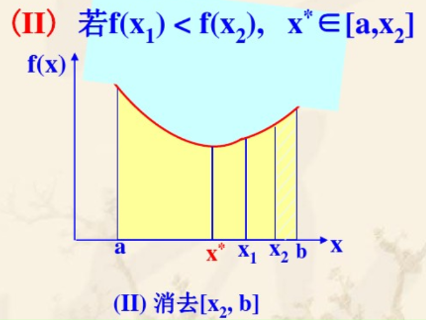
      保留左区间

    3. 若 \(f(x_1) = f(x_2)\) 则 \(x^* \in [x_1,x_2]\)

于是迭代的关键就在于如何取点 \(x_1\) 和 \(x_2\)，下面开始介绍三种取点方法。

基于 python 实现：0.618 法、斐波那契法、二分法 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
class ExactLinearSearch:
    def __init__(self, 
                a: float, b: float, delta: float, 
                f: Callable[[float], float], 
                criterion: str="0.618", max_iter=100) -> None:

        self.a = a
        self.b = b
        self.delta = delta
        self.f = f
        self.max_iter = max_iter

        if criterion == "0.618":
            new_a, new_b, x_star, count = self._f_goad()
        elif criterion == "fibonacci":
            new_a, new_b, x_star, count = self._f_fibo()
        else: # criterion == "binary"
            new_a, new_b, x_star, count = self._f_binary()

        fixed = lambda x, acc: round(x, acc)
        print(f"算法为：“{criterion}” 法")
        print(f"共迭代：{count} 次")
        print(f"左边界: {fixed(new_a, 4)}")
        print(f"右边界: {fixed(new_b, 4)}")
        print(f"最优解: {fixed(x_star, 4)}")
        print(f"最优值: {fixed(f(x_star), 6)}\n")

    def _f_goad(self) -> Tuple[float, float, float, int]:
        a, b, delta, f = self.a, self.b, self.delta, self.f
        count = 0

        lam = a + 0.382 * (b - a)
        mu = b - 0.382 * (b - a)

        while count <= self.max_iter:
            phi_lam = f(lam)
            phi_mu = f(mu)

            if phi_lam <= phi_mu:
                b = mu
            else:
                a = lam

            lam = a + 0.382 * (b - a)
            mu = b - 0.382 * (b - a)

            if b - lam <= delta:
                return a, b, lam, count
            if mu - a <= delta:
                return a, b, mu, count

            count += 1

        return a, b, lam if f(lam) <= f(mu) else mu, count

    def _f_fibo(self) -> Tuple[float, float, float, int]:
        a, b, delta, f, max_iter = self.a, self.b, self.delta, self.f, self.max_iter
        count = None

        F = [0.0] * max_iter
        F[1] = F[2] = 1
        for i in range(3, max_iter):
            F[i] = F[i - 1] + F[i - 2]
            if F[i] >= (b - a) / delta:
                count = i - 2
                break

        if count == None:
            ValueError("区间过大或精度过高导致，找不到合适的迭代次数")

        lam, mu = a, b
        for i in range(3, count + 1):

            lam = a + (1 - F[i - 1] / F[i]) * (b - a)
            mu = b - (1 - F[i - 1] / F[i]) * (b - a)
            if f(lam) <= f(mu):
                b = mu
            else:
                a = lam

        return a, b, lam if f(lam) <= f(mu) else mu, count

    def _f_binary(self) -> Tuple[float, float, float, int]:
        a, b, delta, f, max_iter = self.a, self.b, self.delta, self.f, self.max_iter
        count = None

        count = np.ceil(np.log2((b - a) / delta)).astype(int)

        if count > max_iter:
            ValueError("区间过大或精度过高导致迭代次数过高")

        for _ in range(count):
            c = (a + b) / 2.0
            if f(c) >= 0.0:
                b = c
            else:
                a = c

        return a, b, c, count

1
2
3
4
5
6
7
8
a, b, delta = -1, 1, 0.01
f = lambda x: np.exp(-x) + np.exp(x)  # 原函数
calc_goad = ExactLinearSearch(a, b, delta, f, criterion="0.618")
calc_fibo = ExactLinearSearch(a, b, delta, f, criterion="fibonacci")

a, b, delta = -3, 6, 0.1
f = lambda x: 2 * x + 2               # 导函数
calc_bina = ExactLinearSearch(a, b, delta, f, criterion="binary")

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
算法为：“0.618” 法
共迭代：10 次
左边界: -0.0031
右边界: 0.0069
最优解: 0.0007
最优值: 2.000001

算法为：“fibonacci” 法
共迭代：11 次
左边界: -0.0225
右边界: 0.0
最优解: -0.0139
最优值: 2.000193

算法为：“binary” 法
共迭代：7 次
左边界: -1.0312
右边界: -0.9609
最优解: -0.9609
最优值: 0.078125

0.618 法

基于「函数值」进行选点。

按照黄金分割的比例取点 \(x_1\) 和 \(x_2\)，不断迭代判断 \(f(x_1)\) 和 \(f(x_2)\) 的值，直到 \(b_k-\lambda_k<\delta\) 或 \(\mu_k-a_k<\delta\) 则结束迭代，取最优解 \(x^*\) 为对应的 \(\lambda_k\) 或 \(\mu_k\) 即可。

Fibonacci 法

基于「函数值」进行选点。

第 \(k\) 次迭代的区间长度是上一个区间长度的 \(\frac{F_{n-k}}{F_{n-k+1}}\)​，即：

\[ b_{k+1} - a_{k+1} = \frac{F_{n-k}}{F_{n-k+1}} (b_{k} - a_{k}) \]

经过 \(n\) 次迭代后，得到区间 \([a_n,b_n]\)，且 \(b_n-a_n \le \delta\)，于是可得：

\[ \begin{aligned} b_n-a_n &= \frac{F_1}{F_2}(b_{n-1}-a_{n-1}) \\ &= \frac{F_1}{F_2} \frac{F_2}{F_3}(b_{n-2}-a_{n-2}) \\ &= \cdots \\ &= \frac{F_1}{F_2} \frac{F_2}{F_3} \cdots \frac{F_{n-1}}{F_n}(b_{1}-a_{1}) \\ &= \frac{F_1}{F_n}(b_1-a_1) \le \delta \end{aligned} \]

在已知上界 \(\delta\) 的情况下可以直接计算出 \(n\) 的值，于是迭代 \(n\) 次即可得到最终的步长值 \(\lambda_n\) 或 \(\mu_n\)

3.2.3 二分法

基于「一阶导数」进行选点。

单调性存在于导数上。极值点左边导数 \(<0\)，极值点右边导数 \(>0\)，于是可以进行二分搜索。

3.2.4 插值法

基于「函数值、一阶导数」进行选点。

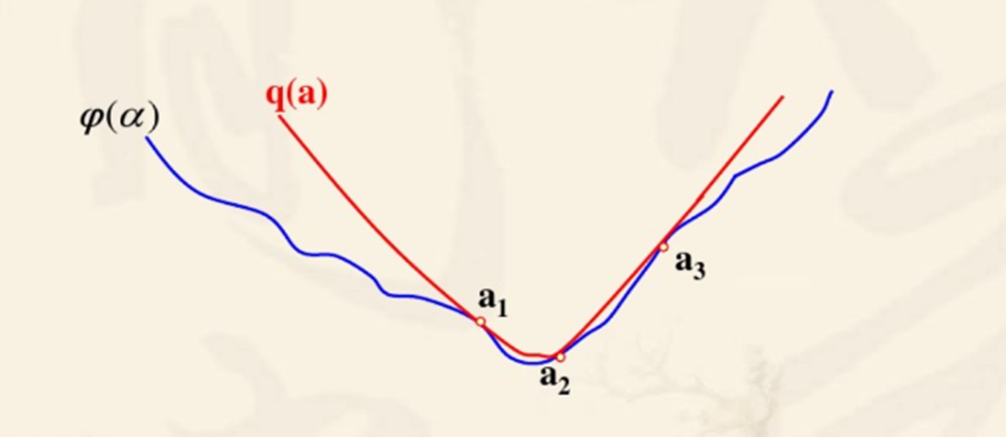
三点二次插值法

三点二次插值法。给定初始迭代区间 \([a_0,b_0]\) 和初始迭代解 \(t_0\)。每次在目标函数上取三个点来拟合一个二次函数，通过拟合出来的二次函数的最小值，来更新三个点为 \(a_1,b_1,t_1\)，直到区间小于上界长度 \(\delta\)，终止迭代，极小值就是当前状态二次函数的最小值。

那么我们如何求解当前状态二次函数的最小值呢？假定三个已知点为 \(x_1<x_2<x_3\)，且 \(f(x_1)>f(x_2)<f(x_3)\)，我们需要知道二次函数的三个参数 \(a,b,c\)，刚好三个已知点可以得到三个方程，从而解出二次函数的三个未知数。

两点二次插值法。只不过少取了一个点，多利用了一个点的导数值来确定二次函数的三个参数罢了，其余迭代过程与三点二次插值完全一致。

不精确线性搜索算法

精确搜索有时会导致搜索时间过长，尤其是当最优解离当前点还很远时。接下来我们介绍不精确线性搜索方法，在确保每一步的函数值都有充分下降的必要条件下，确保收敛并提升计算效率。真的有这么厉害的算法吗？其实根本逻辑很简单，Armijo 准则 限定了搜索方向的上界、Goldstein 准则 在前者的基础上又限定了搜索方向的下界（防止过小导致收敛过慢）、Wolfe 准则 在前者的基础上又完善了下界的约束（确保不会把可行解排除在搜索区间外）

符号定义：我们在已知上一步解 \(x_k\) 和下次迭代的下降方向 \(d_k\) 的基础上，需要寻找合适的 \(\alpha\)。于是唯一变量就是 \(\alpha\)，我们直接定义关于 \(\alpha\) 的一元函数 \(\phi(\alpha) = f(x_k + \alpha d_k)\)，\(g_k\) 表示梯度。

Armijo 准则

只限定搜索上界，给定初始点 \(x_0\)、系数 \(\rho\)：

\[ f(x_k + \alpha d_k) \le \rho \cdot g_k^Td_k \cdot \alpha + f(x_k) \]

Goldstein 准则

又限定了搜索下界，同样给定初始点 \(x_0\)、系数 \(\rho\)：

\[ \begin{aligned} f(x_k + \alpha d_k) \le &\rho \cdot g_k^Td_k \cdot \alpha + f(x_k)\\ f(x_k + \alpha d_k) \ge &(1-\rho) \cdot g_k^Td_k \cdot \alpha + f(x_k) \end{aligned} \]

Wolfe 准则

完善了搜索下界的约束，即保证新点的梯度 \(g_{k+1}^Td_k\) 不低于老点梯度 \(g_{k}^Td_k\) 的 \(\sigma\) 倍。给定 \(x_0,\rho,\sigma\)：

\[ \begin{aligned} f(x_k + \alpha d_k) \le &\rho \cdot g_k^Td_k \cdot \alpha + f(x_k)\\ g(x_k + \alpha_kd_k)^Td_k \ge& \sigma g_{k}^Td_k\\ 0 < \rho < \sigma < 1 \end{aligned} \]

参考：