跳转至

绪论

最优化问题分类

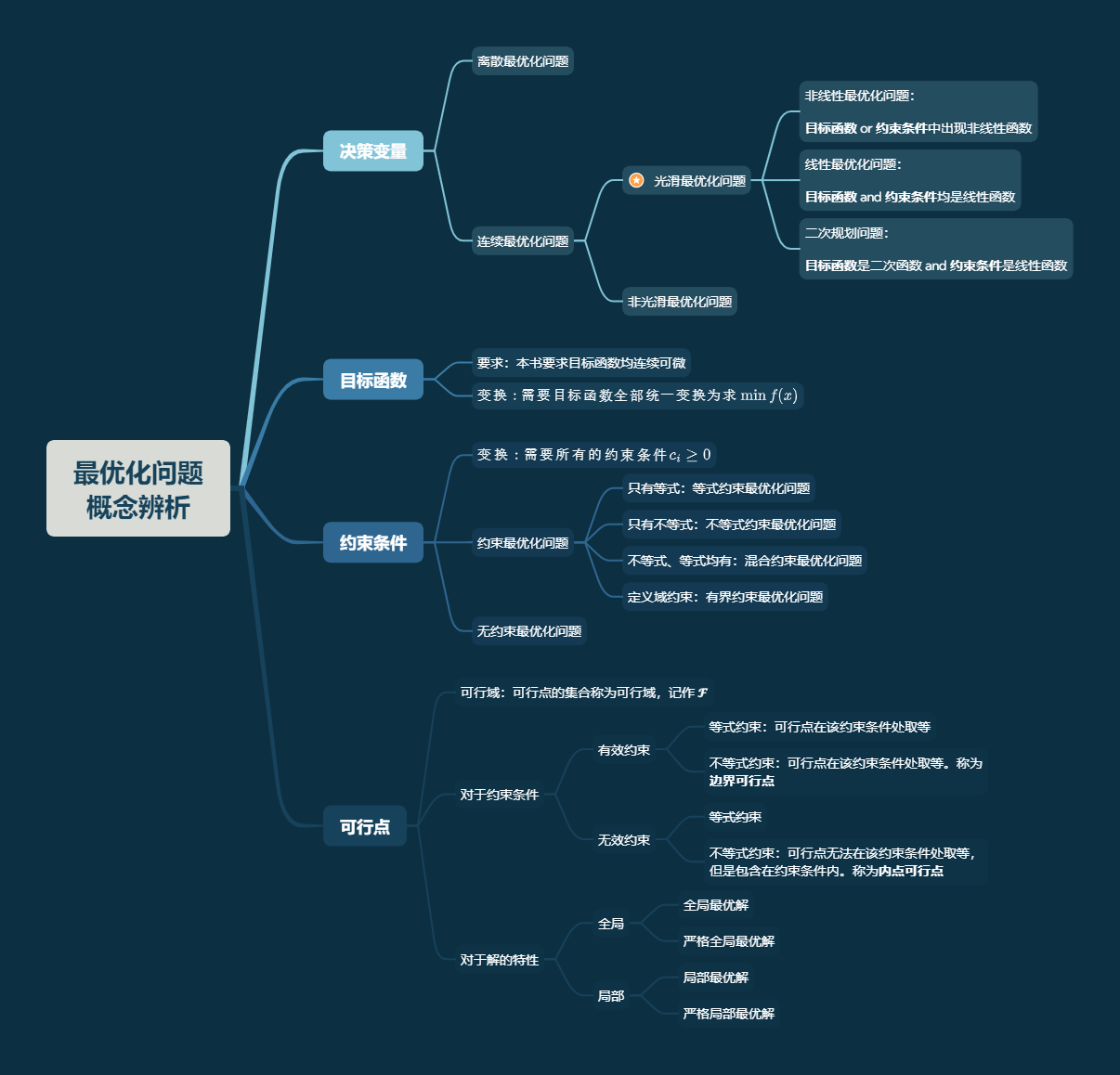
最优化问题分类

最优化问题定义

由于本书介绍的最优化求解方法一般只适用于求解「局部最优解」，那么如何确定「全局最优解」呢？以及如何确定「唯一的全局最优解」呢？

(唯一)全局最优解=局部最优解+(严格)凸目标函数+凸可行域 (\text{唯一})\text{全局最优解}=\text{局部最优解}+(\text{严格})\text{凸目标函数}+\text{凸可行域}

其中凸可行域包含于凸集，凸目标函数包含于凸函数，凸目标函数+凸可行域的问题称为凸规划问题。因此本目将分别介绍凸集、凸函数和凸规划三个概念。

凸集

定义。若集合中任意两点的线性组合都包含于集合，则称该集合为凸集。符号化即：

∀x,y∈D ∧ λ∈[0,1]s.t.λx+(1−λ)y∈D \begin{aligned} \forall \quad x, y \in D \ \land \ \lambda \in [0,1] \\ s.t. \quad \lambda x+(1-\lambda)y \in D \\ \end{aligned}

性质。设 D1,D2⊂RnD_1,D_2 \subset R^n 均为凸集（下列 x,yx,y 均表示向量），则：

  1. 两凸集的交 D1∩D2={x ∣ x∈D1∧x∈D2}D_1 \cap D_2 = \{x\ |\ x \in D_1 \land x \in D_2\} 是凸集；
  2. 两凸集的和 D1+D2={x,y ∣ x∈D1,y∈D2}D_1 + D_2 = \{x,y\ |\ x \in D_1 , y \in D_2\} 是凸集；
  3. 两凸集的差 D1−D2={x,y ∣ x∈D1,y∈D2}D_1 - D_2 = \{x,y\ |\ x \in D_1 , y \in D_2\} 是凸集；
  4. 对于任意非零实数 α\alpha，集合 αD1={αx ∣ x∈D1}\alpha D_1 = \{ \alpha x \ |\ x \in D_1 \}​ 是凸集。

应用。如下两点：

  1. 刻画可行域

    • 凸组合定义

      设 x(1),x(2),⋯ ,x(p)∈Rn,且 ∑i=1pαi=1(ai≥0)s.t.x=α1x1+α2x2+⋯+αpxp则称 x 为向量 x(1),x(2),⋯ ,x(p) 的凸组合 \begin{aligned} \text{设}\ x^{(1)}, x^{(2)}, \cdots, x^{(p)} \in R^n ,\text{且}\ \sum_{i = 1}^p \alpha_i = 1(a_i \ge 0) \\ s.t. \quad x = \alpha_1x^1 + \alpha_2x^2 + \cdots + \alpha_px^p \\ \text{则称}\ x\ \text{为向量}\ x^{(1)}, x^{(2)}, \cdots, x^{(p)}\ \text{的凸组合} \end{aligned}

    • 凸组合定理：D∈RnD \in R^n 是凸集的充分必要条件是 DD 中任取 mm 个点 xi(1,2,⋯m)x^i(1,2,\cdots m) 的凸组合任属于 DD，即：

      ∑i=1mαixi∈D(αi≥0(i=1,2,⋯ ,m),∑i=1mαi=1) \sum_{i = 1}^m \alpha_ix_i \in D\left( \alpha_i \ge 0(i = 1,2,\cdots, m),\sum_{i = 1}^m \alpha_i = 1 \right)
      凸组合定理证明

      凸组合定理证明

  2. 分析最优解的最优性条件

    • 超平面定义（凸集分离定理）：设 D1,D2⊂RnD_1,D_2 \subset R^n 为两非空凸集，若存在非零向量 α∈Rn\alpha \in R^n 和实数 β\beta，使得

      D1⊂H+={x∈Rn ∣ αTx≥β}D2⊂H−={x∈Rn ∣ αTx≤β} \begin{aligned} D_1 \subset H^+ = \{ x \in R^n \ | \ \alpha^T x \ge \beta\} \\ D_2 \subset H^- = \{ x \in R^n \ | \ \alpha^T x \le \beta\} \end{aligned}

      则称超平面 H={x∈Rn ∣ αTx=β}H = \{ x \in R^n \ | \ \alpha^Tx=\beta \} 分离 集合 D1D_1 和 D2D_2，严格分离 时上述不等式无法取等

    • 投影定理：设 D∈RnD \in R^n 是非空闭凸集，y∈Rny \in R^n 但 y∉Dy \notin D，则

      (1)存在唯一的点 x‾∈D,使得集合D到点y的距离最小(2)x‾∈D是点y到集合 D 的最短距离点的充分必要条件为:∀x∈D,<x−x‾,y−x‾>≤0 \begin{align*} (1)& \text{存在唯一的点} \ \overline x \in D,\text{使得集合}D\text{到点} y \text{的距离最小} \\ (2)& \overline x \in D \text{是点} y \text{到集合 D 的最短距离点的充分必要条件为}:\forall x \in D, <x-\overline x,y - \overline x> \le 0 \end{align*}

凸函数

定义。设函数 f(x)f(x) 在凸集 DD 上有定义：

  • 若 ∀x,y∈D 和 λ∈[0,1]\forall x,y \in D\ \text{和}\ \lambda \in [0,1] 有 f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)f(\lambda x + (1-\lambda)y) \le \lambda f(x) + (1-\lambda)f(y)，则称 f(x)f(x) 是凸集 DD 上的凸函数；
  • 若 ∀x,y∈D 和 λ∈(0,1)\forall x,y \in D\ \text{和}\ \lambda \in (0,1) 有 f(λx+(1−λ)y)<λf(x)+(1−λ)f(y)f(\lambda x + (1-\lambda)y) < \lambda f(x) + (1-\lambda)f(y)，则称 f(x)f(x) 是凸集 DD 上的严格凸函数。

性质。如下四点：

  1. 如果 ff 是定义在凸集 DD 上的凸函数，实数 α≥0\alpha \ge 0，则 αf\alpha f 也是凸集 DD 上的凸函数；
  2. 如果 f1,f2f_1,f_2 是定义在凸集 DD 上的凸函数，则 f1+f2f_1+f_2 也是凸集 DD 上的凸函数；
  3. 如果 fi(x)(i=1,2,⋯ ,m)f_i(x)(i=1,2,\cdots,m) 是非空凸集 DD 上的凸函数，则 f(x)=max⁡1≤i≤m∣fi(x)∣f(x) = \max_{1 \le i \le m} |f_i(x)| 也是凸集 DD 上的凸函数；
  4. 如果 fi(x)(i=1,2,⋯ ,m)f_i(x)(i=1,2,\cdots,m) 是非空凸集 DD 上的凸函数，则 f(x)=∑i=1mαifi(x)(αi≥0)f(x) = \displaystyle \sum_{i=1}^m \alpha_i f_i(x)\quad(\alpha_i \ge 0) 也是凸集 DD​ 上的凸函数。

凸函数判定定理。有以下三个角度：

  1. 函数值角度：函数 f(x)f(x) 是 RnR^n 上的凸函数的充分必要条件是 ∀x,y∈Rn\forall x,y \in R^n，单变量函数 ϕ(α)=f(x+αy)\phi(\alpha)=f(x + \alpha y) 是关于 α\alpha 的凸函数

    凸函数的判别定理证明：函数值角度

    凸函数的判别定理证明 - 函数值角度

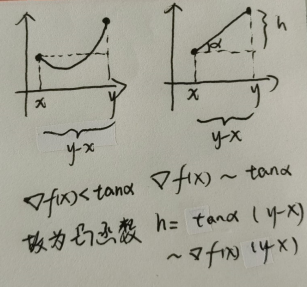
  2. 一阶梯度角度：设 f(x)f(x) 是定义在非空开凸集 DD 上的可微函数，则：

    • f(x)f(x) 是 DD 上凸函数的充分必要条件是：f(y)≥f(x)+∇f(x)T(y−x),∀x,y∈Df(y) \ge f(x)+\nabla f(x)^T(y-x), \quad \forall x,y \in D
    • f(x)f(x) 是 DD 上严格凸函数的充分必要条件是：f(y)>f(x)+∇f(x)T(y−x),∀x,y∈D,x≠yf(y) > f(x)+\nabla f(x)^T(y-x), \quad \forall x,y \in D,\quad x \ne y
    凸函数的判别定理理解性记忆：一阶导数角度

    无需掌握证明，但是为了便于理解性记忆，可以从 二次凸函数 进行辅助理解记忆。

    凸函数的判别定理证明 - 一阶导数角度

  3. 二阶梯度角度：设 f(x)f(x) 是定义在非空开凸集 DD 上的二阶可微函数，则：

    • f(x)f(x) 是 DD 上凸函数的充分必要条件是：海塞矩阵正半定
    • f(x)f(x) 是 DD 上严格凸函数的充分必要条件是：海塞矩阵正定？其实不一定，例如 x4x^4 是严格凸函数，但是其海塞矩阵是正半定的并非正定。因此更严谨的定义应该是：海塞矩阵正定的是严格凸函数，严格凸函数的海塞矩阵是正半定的。

凸规划

本目为个人补充内容，用于整合上述内容。我们知道，学习凸集和凸函数的终极目标是为了求解凸规划问题，凸规划理论可以简述为 「凸可行域 + 凸目标函数 + 局部最优解 = 全局最优解」，那么如何证明这个定理是正确的呢？局部最优解求出来以后，目标函数也确定为凸函数以后，如何确定可行域是凸集呢？下面揭晓：

证明凸规划理论的正确性。如下两条定理：

  1. 定理：在可行域是凸集，目标函数非严格凸的情况下，局部最优解 x∗x^*​ 是全局最优解；

    证明（反证法）

    证明（反证法）

  2. 定理：在可行域是凸集，目标函数是严格凸的情况下，局部最优解 x∗x^* 是「唯一」全局最优解。

    证明（反证法）

    证明（反证法）

确定可行域是否为凸集。如下三条定理：

  1. 定理：若约束条件 ci(x)≥0c_i(x) \ge 0 中每一个约束函数 ci(x)c_i(x) 都是凹函数，则可行域 FF 是凸集；

    证明

    证明

  2. 定理：若约束条件 ci(x)≤0c_i(x) \le 0 中每一个约束函数 ci(x)c_i(x) 都是凸函数，则可行域 FF 是凸集；

    证明

    证明

  3. 定理：若约束条件中每一个约束函数 ci(x)c_i(x) 都恒等于零，则可行域 FF 是凸集。

    证明

    证明

最优性条件

最优性条件是指最优化问题的最优解所必须满足的条件。本目介绍求解 无约束最优化问题 的一阶必要条件和二阶必要条件，再补充介绍二阶充分条件以及针对凸规划问题的二阶充分必要条件。最后简单介绍求解 等式约束最优化问题 的拉格朗日乘子法。

下降方向

在开始之前先简单介绍一下「下降方向」这个概念。

  • 下降方向 定义：设 f(x)f(x) 为定义在空间 RnR^n 的连续函数，点 xˉ∈Rn\bar x \in R^n，若对于方向 s∈Rns \in R^n 存在数 δ>\delta > 0 使

    f(xˉ+αs)<f(xˉ),∀α∈(0,δ) f(\bar x+\alpha s) < f(\bar x),\quad \forall \alpha \in (0,\delta)

    成立，则称 ss 为 f(x)f(x) 在 xˉ\bar x 处的一个下降方向。在 点 xˉ\bar x 处的所有下降方向的全体记为 D(xˉ)D(\bar x)

  • 下降方向 定理：设函数 f(x)f(x) 在点 xˉ\bar x 处连续可微，如存在非零向量 s∈Rns \in R^n 使

    ∇f(xˉ)Ts<0 \nabla f(\bar x)^Ts < 0

    成立，则 ss 是 f(x)f(x) 在点 xˉ\bar x 处的一个下降方向

    证明

    证明

充分必要条件

设 f:D⊂Rn→R1f:D \subset R^n \to R^1 是定义在开集 DD 上的函数，x∗∈Dx^* \in D 是该函数的局部极小点，f(x)f(x) 的一阶导数 g(x)=∇f(x)g(x)=\nabla f(x)，二阶导数 G(x)=∇2f(x)G(x)=\nabla ^2f(x)。

一阶必要条件。若目标函数在定义域 D 上连续可微，则 x∗x^* 是局部极小点的一阶必要条件为：

g(x∗)=0 g(x^*)= 0

二阶必要条件。若目标函数在定义域 D 上二阶连续可微，则 x∗x^* 是局部极小点的二阶必要条件为：

g(x∗)=0,G(x∗)≥0 g(x^*)= 0,\quad G(x^*)\ge 0

二阶充分条件。若目标函数在定义域 D 上二阶连续可微，则 x∗x^* 是「严格」局部极小点的二阶充分条件为：

g(x∗)=0,G(x∗) 是正定的 g(x^*)= 0,\quad G(x^*) \text{ 是正定的}

充分必要条件（凸最优性定理）。在无约束最优化问题中，如果目标函数是凸的，则 x∗x^* 是全局极小点的充分必要条件是：

g(x∗)=0 g(x^*)= 0

最优化方法概述

现实生活中，对于常见问题的建模往往是极其复杂的，为了求得最优解，我们需要对建立的模型进行微分算子的求解。但是问题是，尽管我们知道最优解一定存在于微分算子的数值解中，但是我们往往不能很快的计算出其数值解，因此我们需要采用别的方法进行计算。最常用的方法就是本书介绍的迭代法。

大概就两步：确定初值开始判断，如果符合条件的约束则停止迭代得到最终的解；如果不符合约束则对当前迭代值赋予修正量并继续迭代判断。直到找到最终的解。接下来将对 5 个专有名词进行解释，分别为：初始点的选取、迭代点好坏的判定、收敛速度、迭代的终止条件、修正量 s(k)s^{(k)} 的确定。

初始点的选取

初始点的选取取决于算法的收敛性能。

  • 如果一个算法可以做到全局收敛，则初始点的选取是任意的
  • 如果一个算法只能局部收敛，则初始点的选取往往需要尽可能的接近最优解，而这往往是困难的，因为我们并不知道的最优解是什么。此时可以采用借鉴之前的经验来选择初始点

迭代点好坏的判定

判定一个迭代点的好坏时，我们往往会设计一个评价函数，而评价函数的设计取决于约束问题的种类。

  • 对于无约束最优化问题。我们可以直接将目标函数 f(x)f(x) 设计为评价函数。很显然，如果一个迭代点对应的的函数值比之前点对应的函数值更小，则可以说明当前迭代点由于之前的点
  • 对于有约束最优化问题。此时我们不仅仅需要考虑函数值的大小，也要考虑当前迭代点的可行程度（离可行域的距离）。因此此类最优化问题往往既包含目标函数，也包含约束函数。

收敛速度

若当前算法一定收敛，我们还需要判断收敛的速度，接下来介绍收敛的速度。

假设

  • 设向量序列 {x(k)⊂Rn}\{ x^{(k)} \subset R^n \} 收敛于 x∗x^*​

定义

  1. 误差序列：ek=x(k)−x∗e_k = x^{(k)} - x^*
  2. 收敛率表达式：lim⁡k→∞∣∣ek+1∣∣∣∣ek∣∣r=C\displaystyle \lim_{k \to \infty} \frac{|| e_{k+1} ||}{||e_k||^r} = C，并称序列 {x(k)}\{x^{(k)}\} 的 rr 阶以 CC 为因子收敛于 x∗x^*

线性收敛

  • 定义：r=1,0<C<1r=1,0 < C<1
  • 性质：CC 越小，算法收敛越快

超线性收敛

  • 定义：r=1,C=0r=1,C=0

  • 定理：r>1r>1​ 时的算法均为超线性收敛算法

    证明

    证明

迭代的终止条件

对于收敛速度比较慢的算法。根据一阶必要条件，我们知道最优解一定取在微分算子为 0 的向量上，因此我们以下式为终止条件是一种可行的选择：

∣∣∇f(x(k)∣∣≤ϵ ||\nabla f(x^{(k)}|| \le \epsilon

但是问题在于这对收敛速度很快的算法不使用，如下图的无约束最优化问题。已知两个局部最优解分别为 x1∗,x2∗x_1^*,x_2^*，迭代的两个解分别为 x‾1,x‾2\overline{x}_1,\overline{x}_2，可以看出：尽管 2 号点相对于 1 号点更靠近局部最优解，但是由于 2 号点的梯度更大，明显不如 1 号点更加局部最优，因此利用微分算子作为迭代的终止条件不适用于收敛速度快的算法

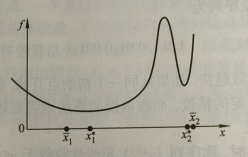
无约束最优化问题

对于超线性收敛的算法。一个理想的收敛终止条件为 ∣∣x(k)−x∗∣∣≤ϵ||x^{(k)} - x^*|| \le \epsilon，但是由于最优解 x∗x^* 是未知的，因此该方案不可行，同理 f(x∗)f(x^*) 也是未知的，因此 ∣∣f(x(k))−f(x∗)∣∣≤ϵ||f(x^{(k)}) - f(x^*)|| \le \epsilon 也是不可行的。那么有没有什么替代的方案呢？答案是有的。

  1. 方案一：利用「函数解序列」进行替代。即以下式作为迭代的终止条件

    ∣∣x(k+1)−x(k)∣∣≤ϵ || x^{(k+1)} - x^{(k)} || \le \epsilon
    证明

    证明

  2. 方案二：利用「函数值序列」进行替代。即以下式作为迭代的终止条件

    ∣∣f(x(k+1))−f(x(k))∣∣≤ϵ || f(x^{(k+1)}) - f(x^{(k)}) || \le \epsilon
    证明

    证明

  3. 一般情况下，对于上述超线性算法的判断收敛的方法，只用其中一种往往不适当。此时一般使用两种方法集成的思路进行判断。

修正量的确定

本书介绍的迭代修正值都是使得当前迭代后的值小于上一个状态的函数值，我们称这类使评价函数值下降的算法为「单调下降算法」。至于如何得出修正量，我们往往通过求解一个相对简单易于求解的最优化问题（通常成为子问题），来计算获得修正量。