无约束优化方法

本章介绍无约束函数的最优化算法。其中：

• 梯度下降法基于「一阶梯度」。最基本的方法；
• 牛顿法基于「二阶梯度」。最主要的方法；
• 共轭梯度法基于「一阶梯度」。解大型最优化问题的首选；
• 拟牛顿法基于「函数值和一阶梯度」。其中的 BFGS 是目前最成功的方法。

Python 实战：极小化 Rosenbrock 函数

Python

# 目标函数
def f(x: np.ndarray) -> float:
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 一阶梯度
def g(x: np.ndarray) -> np.ndarray:
    grad_x = -2 * (1 - x[0]) - 400 * x[0] * (x[1] - x[0]**2)
    grad_y = 200 * (x[1] - x[0]**2)
    return np.array([grad_x, grad_y])

# 二阶梯度
def G(x: np.ndarray) -> np.ndarray:
    grad_xx = 2 - 400 * x[1] + 1200 * x[0]**2
    grad_xy = -400 * x[0]
    grad_yx = -400 * x[0]
    grad_yy = 200
    return np.array([
        [grad_xx, grad_xy],
        [grad_yx, grad_yy]
    ])

# 初始点
initial_point = [-1.2, 1]

已知最优点为 \(x^*=(1, 1)^T\)，最优解 \(f(x^*)=0\)，以书中例题初始点 \((-1.2,1)^T\) 为例开始迭代。

梯度下降法牛顿法共轭梯度法拟牛顿法

Python

def gradient_descent(initial_point, max_iter=5, eps=1e-6):
    x = np.array(initial_point)
    points = [x]
    gradients = [g(x)]
    alphas = []

    for _ in range(max_iter):
        grad = gradients[-1]

        # 搜索方向
        direction = -grad

        # 步长因子：无法确定准确的步长最小化函数，因此此处采用二分法搜索最优步长
        alpha = 1
        while f(x + alpha * direction) > f(x):
            alpha /= 2

        x = x + alpha * direction
        points.append(x)
        gradients.append(g(x))
        alphas.append(alpha)

        if np.linalg.norm(grad) < eps:
            break

    return points, gradients, alphas

points, gradients, alphas = gradient_descent(initial_point, max_iter=100, eps=1e-6)

for i, (point, grad, alpha) in enumerate(zip(points, gradients, [1] + alphas)):
    print(f"Iteration {i}:")
    print(f"  Point       = {point}")
    print(f"  Gradient    = {grad}")
    print(f"  Step Size   = {alpha}")
    print(f"  Direction   = {-grad}")
    print(f"  Function Val= {f(point)}\n")

迭代 100 次后输出为：

Text Only

Iteration 98:
Point       = [0.93432802 0.87236513]
Gradient    = [ 0.0942865  -0.12074477]
Step Size   = 0.00390625
Direction   = [-0.0942865   0.12074477]
Function Val= 0.004349256784446673

Iteration 99:
Point       = [0.93414387 0.87260096]
Gradient    = [-0.12281587 -0.00476179]
Step Size   = 0.001953125
Direction   = [0.12281587 0.00476179]
Function Val= 0.004337086557103718

Iteration 100:
Point       = [0.93438374 0.87261026]
Gradient    = [ 0.04171114 -0.09254423]
Step Size   = 0.001953125
Direction   = [-0.04171114  0.09254423]
Function Val= 0.004326904052586884

Python

def newton_method(initial_point, max_iter=5, eps=1e-6):
    x = np.array(initial_point)
    points = [x]
    gradients = [g(x)]
    Hessians = [G(x)]

    for _ in range(max_iter):
        grad = gradients[-1]
        Hessian = Hessians[-1]

        # 搜索方向
        direction = np.linalg.inv(Hessian) @ grad

        # 步长因子：假定使用固定步长的牛顿法
        alpha = 1

        x = x - alpha * direction
        points.append(x)
        gradients.append(g(x))
        Hessians.append(G(x))

        if np.linalg.norm(grad) < eps:
            break

    return points, gradients, Hessians

points, gradients, Hessians = newton_method(initial_point, max_iter=50, eps=1e-6)

for i, (point, grad, Hessian) in enumerate(zip(points, gradients, Hessians)):
    print(f"Iteration {i}:")
    print(f"  Point       = {point}")
    print(f"  Gradient    = {grad}")
    print(f"  Hessian     = {Hessian}")
    print(f"  Function Val= {f(point)}\n")

迭代 7 次即收敛：

Makefile

Iteration 5:
Point       = [0.9999957  0.99999139]
Gradient    = [-8.60863343e-06 -2.95985458e-11]
Hessian     = [[ 801.99311306 -399.99827826]
[-399.99827826  200.        ]]
Function Val= 1.8527397192178054e-11

Iteration 6:
Point       = [1. 1.]
Gradient    = [ 7.41096051e-09 -3.70548037e-09]
Hessian     = [[ 802.00000001 -400.        ]
[-400.          200.        ]]
Function Val= 3.4326461875363225e-20

Iteration 7:
Point       = [1. 1.]
Gradient    = [-0.  0.]
Hessian     = [[ 802. -400.]
[-400.  200.]]
Function Val= 0.0

Python

def conjugate_gradient(initial_point, max_iter=5, eps=1e-6):
    x = np.array(initial_point)
    points = [x]
    gradients = [g(x)]
    directions = [-g(x)]
    alphas = []

    for i in range(max_iter):
        grad = gradients[-1]

        # 搜索方向：FR公式
        if i == 0:
            direction = -grad
        else:
            beta = np.dot(g(x), g(x)) / np.dot(g(points[-2]), g(points[-2]))
            direction = -g(x) + beta * direction

        # 步长因子：精确线搜索直接得到闭式解
        alpha = -np.dot(grad, direction) / np.dot(direction, G(x) @ direction)

        x = x + alpha * direction

        directions.append(direction)
        alphas.append(alpha)
        points.append(x)
        gradients.append(g(x))

        if np.linalg.norm(grad) < eps:
            break

    return points, gradients, alphas

points, gradients, alphas = conjugate_gradient(initial_point, max_iter=1000, eps=1e-6)

for i, (point, grad, alpha) in enumerate(zip(points, gradients, alphas)):
    print(f"Iteration {i}:")
    print(f"  Point       = {point}")
    print(f"  Gradient    = {grad}")
    print(f"  Step Size   = {alpha}")
    print(f"  Direction   = {-grad}")
    print(f"  Function Val= {f(point)}\n")

迭代 1000 次后输出为：

Makefile

Iteration 997:
Point       = [0.9999994  0.99999875]
Gradient    = [ 1.90794906e-05 -1.01414007e-05]
Step Size   = 0.0005161468619784313
Direction   = [-1.90794906e-05  1.01414007e-05]
Function Val= 6.191018745155016e-13

Iteration 998:
Point       = [0.99999931 0.99999861]
Gradient    = [ 5.43686111e-06 -3.40374227e-06]
Step Size   = 0.0005078748917694624
Direction   = [-5.43686111e-06  3.40374227e-06]
Function Val= 4.986125950068217e-13

Iteration 999:
Point       = [0.9999993 0.9999986]
Gradient    = [ 1.34784246e-06 -1.36924747e-06]
Step Size   = 0.0005356250138048412
Direction   = [-1.34784246e-06  1.36924747e-06]
Function Val= 4.881643528976312e-13

Python

def bfgs(initial_point, max_iter=5, eps=1e-6):
    x = np.array(initial_point)
    points = [x]
    gradients = [g(x)]
    B = G(x)

    for _ in range(max_iter):
        grad = gradients[-1]

        # 迭代公式
        x = x - np.linalg.inv(B) @ grad

        # 更新 B 矩阵
        s = x - points[-1]
        y = g(x) - gradients[-1]
        B = B + np.outer(y, y) / (s @ y) - (B @ np.outer(s, s) @ B) / (s @ B @ s)

        points.append(x)
        gradients.append(g(x))

        if np.linalg.norm(grad) < eps:
            break

    return points, gradients

points, gradients = bfgs(initial_point, max_iter=1000, eps=1e-6)

for i, (point, grad) in enumerate(zip(points, gradients)):
    print(f"Iteration {i}:")
    print(f"  Point       = {point}")
    print(f"  Gradient    = {grad}")
    print(f"  Function Val= {f(point)}\n")

迭代 78 次收敛：

Makefile

Iteration 76:
Point       = [1.00000075 0.99999921]
Gradient    = [ 0.000918   -0.00045825]
Function Val= 5.255482679080297e-10

Iteration 77:
Point       = [1.00000006 1.00000012]
Gradient    = [ 6.46055099e-07 -2.63592925e-07]
Function Val= 3.7061757712619374e-15

Iteration 78:
Point       = [1. 1.]
Gradient    = [6.75185684e-10 4.68913797e-10]
Function Val= 6.510026595267928e-19

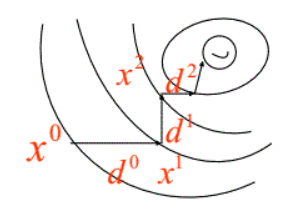
梯度下降法

放一张生动的图 ¹：

迭代公式如下：

\[ x_{k+1} = x_k - \alpha_k \nabla f(x_k) \]

每次迭代时，下降方向 \(d_k\) 采用当前解 \(x_k\) 处的负梯度方向 \(- \nabla f(x_k)\)，步长因子 \(\alpha_k\) 通过 线性搜索 计算得到。

结论：相邻迭代解 \(x_k\) 和 \(x_{k+1}\) 的方向 \(d_k\) 和 \(d_{k+1}\) 是正交的。如下图所示：

证明：由于 \(\phi(\alpha) = f(x_k + \alpha d_k)\)，在采用线性搜索找最优步长时，步长的搜索结果 \(\alpha_k\) 即为使得 \(\phi'(\alpha)=0\) 的解，于是可得 \(0=\phi'(\alpha) = \phi'(\alpha_k) = \nabla f(x_k+\alpha_k d_k)d_k = -d_{k+1}^T \cdot d_k\)，即 \(d_{k+1}^T \cdot d_k = 0\)。

也正因为搜索方向正交的特性导致梯度下降法的收敛速度往往不尽如人意。优点在于程序设计简单并且计算和存储量都不大，以及对初始点的要求不高。

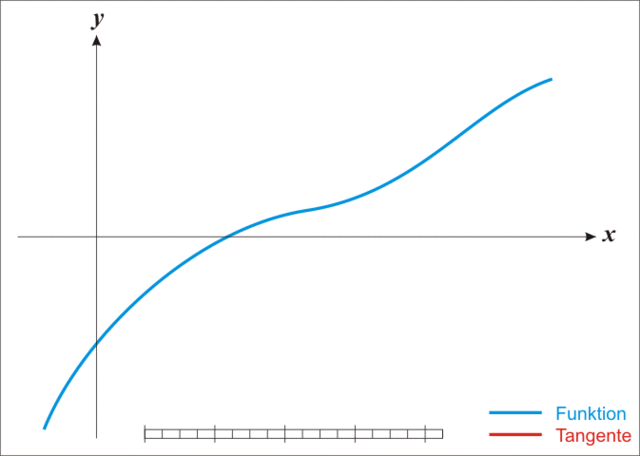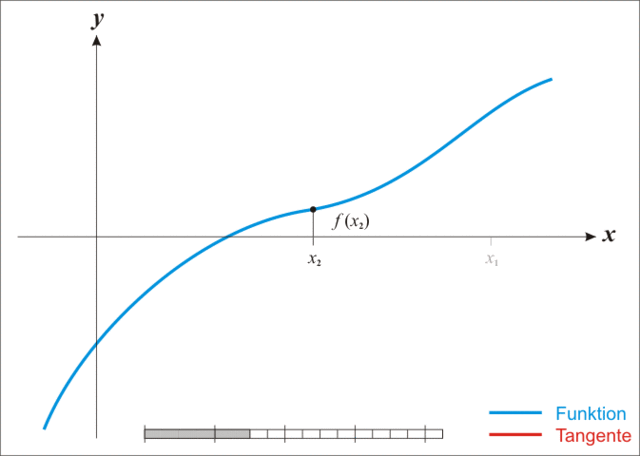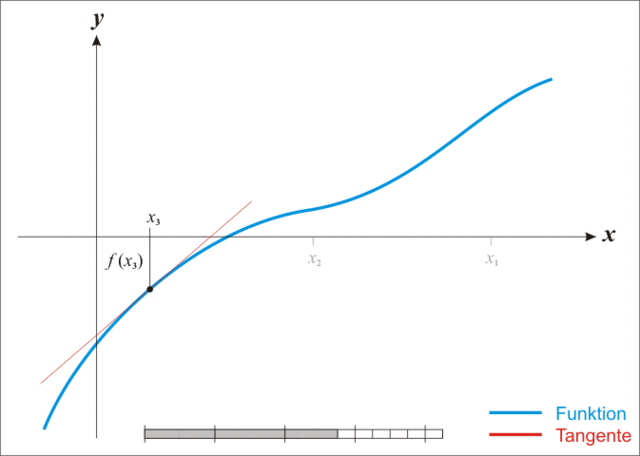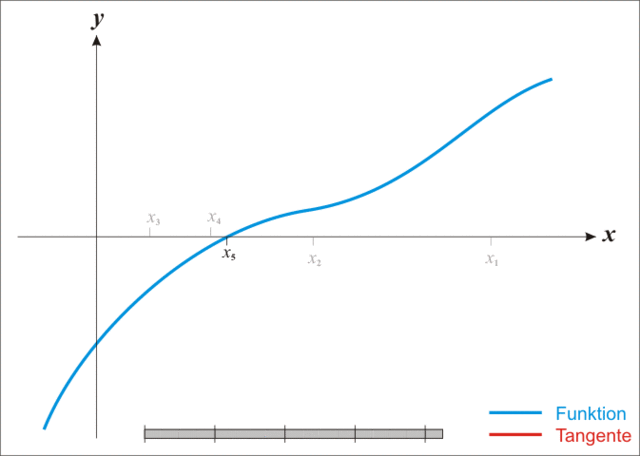
牛顿法

放一张生动的图：

*注：本图演示的是求解一维函数零点的迭代过程，需要使得 \(f(x)=0\)，因此比值式为原函数除以导函数。后续介绍的是极小化函数的过程，需要使得 \(f'(x)=0\)，因此比值式为一阶导数除以二阶导数，高维就是二阶梯度的逆乘以一阶梯度。

迭代公式：

\[ x_{k+1} = x_k - \nabla^2f(x_k)^{-1}\nabla f(x_k) \]

牛顿法相较于梯度下降法有了更快的收敛速度，但是由于需要计算和存储海塞矩阵导致计算量增加并且有些目标函数可能根本求不出二阶梯度。同时牛顿法对于初始迭代点的选择比梯度下降法要苛刻的多。

共轭梯度法

我们利用共轭梯度法解决「正定二次函数」的极小化问题。由于梯度下降法中相邻迭代点的方向是正交的导致搜索效率下降，牛顿法又由于需要计算和存储海塞矩阵导致存储开销过大，共轭梯度法的核心思想是 相邻两个迭代点的搜索方向是关于正定二次型的正定阵正交的。这样既保证了迭代收敛的速度也避免了计算存储海塞矩阵的开销。美中不足的是当共轭梯度法解决其他问题是往往会出现对线搜索的过度依赖，一旦线搜索变差会导致整个迭代过程精度变差。

概念补充：

• 共轭的定义：\(x\) 与 \(y\) 共轭当且仅当 \(x^TGy=0\)，其中 G 为对称正定阵；
• 正定二次函数：形如 \(f(x) =\frac{1}{2} x^TGx - b^Tx + c\) 的函数。

给定初始迭代点 \(x_0\)，收敛阈值 \(\epsilon\)，迭代公式仍然是 \(x_{k+1} = x_k + \alpha_k d_k\)，即：

\[ \begin{aligned} x_{k+1} =& x_k + \alpha_k d_k\\ =& x_k + (-\frac{g_k^T d_k}{d_k^TGd_k}) (-g_k + \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} d_{k-1}) \end{aligned} \]

下面分别推导步长因子 \(\alpha_k\)​ 和搜索方向 \(d_k\)。

1）确定步长因子 \(\alpha_k\)。推导公式如下：

\[ \begin{aligned} \alpha &= \min_{\alpha} \phi(\alpha) \\ &= \min_{\alpha} f(x_k+\alpha d_k) \\ &= \min_{\alpha} \frac{1}{2}(x_k+\alpha d_k)^TG(x_k+\alpha d_k) - b^T(x_k+\alpha d_k) + c \\ &= \min_{\alpha} \frac{1}{2} (x_k^TGx_k + 2\alpha x_k^T G d_k + \alpha^2d_K^Td_k) - b^Tx_k - b^T \alpha d_k + c\\ &= \min_{\alpha} \frac{1}{2} x_k^TGx_k + \alpha x_k^T G d_k + \frac{1}{2}\alpha^2d_k^T G d_k - b^T \alpha d_k + c \end{aligned} \]

由于目标函数是正定二次型，显然可以直接求出步长因子的闭式解：

\[ \begin{aligned} \frac{d \phi(\alpha)}{d\alpha} &= x_k^T G d_k + \alpha d_k^T G d_k - b^Td_k \\ &= 0 \end{aligned} \]

于是可以导出当前的步长因子 \(\alpha_k\) 的闭式解为：

\[ \begin{aligned} \alpha_k &= \frac{(b^T - x^TG)d_k}{d_k^TGd_k} \\ &= -\frac{g_k^T d_k}{d_k^TGd_k} \end{aligned} \]

2）确定搜索方向 \(d_k\)。推导公式如下：

\[ d_k = -g_k + \beta d_{k-1} \]

可见只需要确定组合系数 \(\beta\)。由于共轭梯度法遵循相邻迭代点的搜索方向共轭，即 \(d_{k-1}^TGd_k=0\)，因此对上式两侧同时左乘 \(d_{k-1}^TG\)，有：

\[ \begin{aligned} d_{k-1}^TGd_k &= -d_{k-1}^TGg_k + \beta d_{k-1}^TGd_{k-1} \\ &= 0 \end{aligned} \]

于是可得当前的组合系数 \(\beta\) 为：

\[ \beta = \frac{d_{k-1}^TGg_k}{d_{k-1}^TGd_{k-1}} \]

上述组合系数 \(\beta\) 的结果是共轭梯度最原始的表达式，后人又进行了变形，给出 FR 的组合系数表达式（这一步暂时没证出来）：

\[ \begin{aligned} \beta = \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} \end{aligned} \]

当然了由于初始迭代时没有前一个搜索方向，因此直接用初始点的梯度作为搜索方向，即：

\[ d_0 =-g_0 \]

于是可以导出当前的搜索方向 \(d_k\) 的闭式解为：

\[ d_k = -g_k + \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} d_{k-1} \]

拟牛顿法

梯度下降法和牛顿法都可以统一成下面的表达式：

\[ x_{k+1} = x_k - \alpha_k B_k \nabla f(x_k) \]

• 梯度下降法的步长因子通过精确线搜索获得，海塞矩阵的逆 \(B_k\) 不存在，可以看做为单位阵 \(E\)
• 牛顿法的步长因子同样可以通过精确线搜索获得，当然也可以设置为定值，海塞矩阵的逆 \(B_k\) 对应二阶梯度的逆 \((\nabla^2 f(x_k))^{-1}\)

前者收敛速度差、后者计算量和存储量大，我们尝试构造一个对称正定阵 \(B_k\) 来近似代替二阶梯度的逆，即 \(B_k \approx (\nabla^2 f(x_k))^{-1}\)，使得该法具备较快的收敛速度与较少的内存开销。

介绍最著名的 BFGS 拟牛顿法，它的核心思想是每次迭代过程中对其进行快速校正，从而在确保收敛速度的情况下提升计算效率。迭代公式如下：

\[ \begin{aligned} &x_{k+1} = x_k - B_k^{-1}g_k \\ &\text{记: } \begin{cases} s_k = x_{k+1} - x_k\\ y_k = g_{k+1} - g_k \end{cases}\\ &\text{则: } \begin{cases} B_0 = \nabla^2f(x_0)\\ \displaystyle B_{k+1} = B_k + \frac{y_ky_k^T}{s_k^Ty_k} - \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k} \end{cases} \end{aligned} \]

参考：

• 西北工业大学 - 课件 - 含例题与解析
• 北京大学 - 教材 - 含例题与解析
• 路人 - 博客 - 更通俗的解释
• 牛顿法 - wiki - 更权威的解释

实例：最小二乘建模策略

前面介绍了很多求解模型参数的方法，但如何建模却未曾提及。这里我们就以最小二乘法为例，展示一个问题从建模到求解的全过程。

模型建立

假设现在拥有 \(m\) 个独立同分布的观察数据，包含特征 \(\mathbf A_{m\times n}\) 与标签 \(\mathbf b\)。我们希望找到一个模型 \(f(\mathbf x)\) 来近似表示特征到标签的映射，就可以采用最小二乘法 ² 来建立模型。其核心思想是最小化模型预测值与真实标签值之间的平方损失。

具体地，利用最小二乘法建立的模型可以定义为：

\[ \min_{\mathbf x\in R^n}f(\mathbf x) = \min \frac{1}{2} { \sum_{i = 1}^m [f(\mathbf x) - b_i]^2 },\quad m\ge n \]

将残量函数/残差记作 \(r(\mathbf x)\)，即 \(r_i(\mathbf x)=f(\mathbf x)-b_i\)，那么利用最小二乘法建立的模型就可以简记为：

\[ \begin{aligned} \min_{\mathbf x\in R^n}f(\mathbf x)=\min \frac{1}{2}\sum_{i = 1}^m [r_{i}(\mathbf x)]^2,\quad m\ge n \end{aligned} \]

当 \(r_i(\mathbf x)\) 为线性函数时，当前问题为线性最小二乘问题；当 \(r_i(\mathbf x)\) 为非线性函数时，当前问题为非线性最小二乘问题。下面分别讨论这两种情况的求解策略。

线性模型求解

此时可以直接将目标函数写成：

\[ \begin{aligned} \min f(\mathbf x)&=\frac{1}{2}|| \mathbf A\mathbf x-\mathbf b ||^2\\ &= \frac{1}{2}\mathbf x^T\mathbf A^T\mathbf A\mathbf x-\mathbf b^T\mathbf A\mathbf x+\frac{1}{2}\mathbf b^T\mathbf b \end{aligned} \]

利用一阶必要条件：

\[ \begin{aligned} \nabla f(\mathbf x)= \mathbf A^T\mathbf A\mathbf x - \mathbf A^T\mathbf b = 0 \end{aligned} \]

想要求解其中的 \(\mathbf x\)，本质上就是解一个线性方程。可以分别使用 Cholesky 分解、QR 分解、SVD 分解等方法快速计算最优解 \(\mathbf x^*\)。

非线性模型求解

这里引入一种全新的优化算法：高斯牛顿法，该方法对应的迭代解的公式如下：

\[ x^{k+1}= x^k - (A_k^TA_k)^{-1}A_k^Tr_k \]

其中：

\[ \begin{aligned} A_k = \begin{bmatrix} \nabla r_1(x_k)\\ \nabla r_2(x_k)\\ \vdots \\ \nabla r_m(x_k) \end{bmatrix},\quad r_k = \begin{bmatrix} r_1(x_k)\\ r_2(x_k)\\ \vdots \\ r_m(x_k) \end{bmatrix}\\ \end{aligned} \]

*注：用模型进行预测时的自变量与求解模型参数时的自变量不是同一个东西

模型在建立时需要确定具体的项，其中的参数都只是项的系数，因此模型求解求的其实也都是系数。例如我们建立了一个形如下式的模型：

\[ f(\mathbf x;\boldsymbol \theta)=\theta_1 x_1+e^{\theta_2x_2} \]

其中 \(\mathbf x\) 为观测特征，\(\boldsymbol \theta\) 为模型参数。

• 在求解模型时，我们拥有大量的 \(\mathbf x\) 作为训练数据（也就是上文的 \(\mathbf A\) 矩阵），将其中的 \(\boldsymbol \theta\) 看作自变量进行迭代求解；
• 在用模型进行预测时，此时 \(\boldsymbol \theta\) 已经全部求解出来了，那么每一个观测数据 \(\mathbf x\) 就是自变量。

---

1. The keys of Deep Learning in 100 lines of code | Javier Ideami - (medium.com) ↩

2. 非线性最小二乘 | 王金戈 - (zhuanlan.zhihu.com) ↩