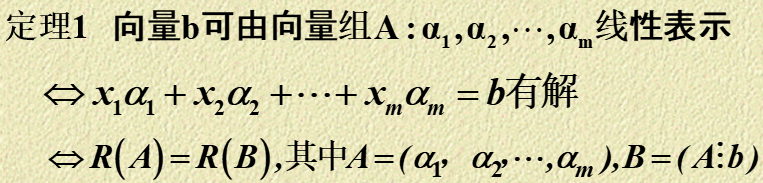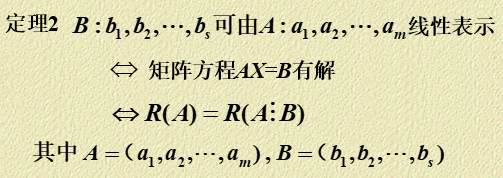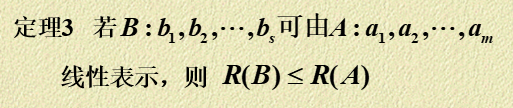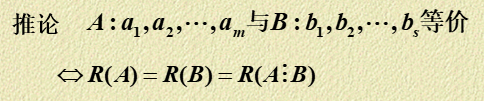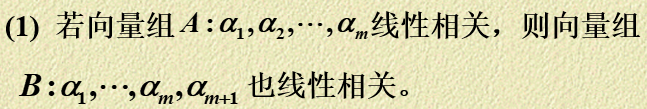向量组

现在我们从向量的角度来理解矩阵。

基本概念

向量、向量组和矩阵

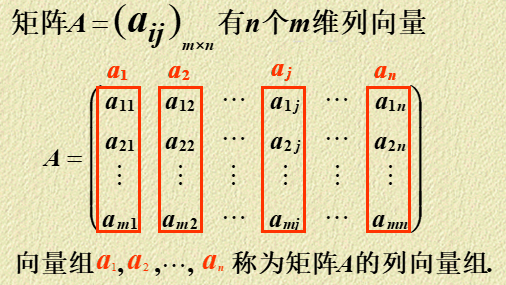
向量就是一个有向线段，显然当向量的元素个数超过 3 时就无法用直观的几何来表示，而向量组就是元素个数相等的列/行向量的集合，而矩阵就可以看作一个向量组。矩阵和向量组的关系如下图所示：

线性组合和线性表示

线性组合的定义。给定向量组 \(\mathbf {A}: \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\)，对于任何一组实数 \(k_1,k_2,\cdots,k_n\)，向量 \(k_1\mathbf a_1+k_2\mathbf a_2+\cdots+k_n\mathbf a_n\) 称为向量组的一个线性组合，\(k_1,k_2,\cdots,k_n\) 称为这个线性组合的系数。

线性表示的定义。给定向量组 \(\mathbf {A}: \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\) 和向量 \(\mathbf b\)，如果存在一组数 \(\lambda_1,\lambda_2,\cdots,\lambda_n\)，使 \(\mathbf b=\lambda_1\mathbf a_1+\lambda_2\mathbf a_2+\cdots+\lambda_n\mathbf a_n\)，则称向量 \(\mathbf b\) 是向量组 \(\mathbf A\) 的线性组合或称向量 \(\mathbf b\) 能由向量组 \(\mathbf A\) 线性表示。

线性表示的判定。转化为方程组是否有解的判定，进而转化为求解矩阵的秩的问题。有以下三种情况：

1）判定向量 \(\mathbf b\) 能否被向量组 \(\mathbf A\) 线性表示。\(\mathbf b\) 可由 \(\mathbf {A}: \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\) 线性表示当且仅当 Ax=b 有解

2）判定向量组 \(\mathbf B\) 能否被向量组 \(\mathbf A\) 线性表示：

该判定定理有以下推论：

3）判定向量组 \(\mathbf B\) 与向量组 \(\mathbf A\) 等价：

向量组的线性相关性

定义：

判定：

• 定理一：

  

  证明：按照定义，只需要移项 or 同除，进行构造即可

• 定理二：

  

  证明：按照定义，转化为齐次线性方程组解的问题

  • 有非零解 \(\Leftrightarrow\) 无数组解（将解方程取倍数即可），\(R(A)=R(A,0)<m\)
  • 仅有零解 \(\Leftrightarrow\) 唯一解，\(R(A)=R(A,0)=m\)

结论：

• 结论一：

  

  证明：\(R(A)<m \to R(B)\le R(A)+1 <m+1\)

• 结论二：

  

  证明：\(R(A_{x\times m})=m \to R\binom{A}{b}=m\)

• 结论三：

  

  证明：\(R(A)\le n <m\)

• 结论四：

  

  证明：\(R(A)=m,R(A,b)<m+1 \to Ax=b\text{有唯一解}\)

  • \(\max \{ R(A),R(b) \} \le R(A,b) \le m+1 \to m \le R(A,b) \le m+1\)
  • 又 \(R(A,b)<m+1\)
  • 故 \(R(A,b)=m\)
  • 因此 \(R(A)=R(A,b)=m \to \text{有唯一解}\)

向量组的秩

最大无关组的定义

定义一：

注意：

• 最大无关组之间等价
• 最大无关组 \(A_0\) 和原向量组 \(A\) 等价

定义二：

向量组的秩和矩阵的秩的关系

向量组的秩的结论

证明：全部可以使用矩阵的秩的性质进行证明

向量空间

向量空间的定义

可以从高中学到的平面向量以及空间向量入手进行理解，即平面向量就是一个二维向量空间，同理空间向量就是一个三维向量空间，那么次数就是拓展到 n 维向量空间，道理是一样的，只不过超过三维之后就没有直观的效果展示罢了。

向量空间的基与维数

同样可以从高中学到的向量入手，此处的基就是基底，维数就是有几个基底。所有的基之间都是线性无关的，这是显然的。然后整个向量空间中任意一个向量都可以被基线性表示，也就很显然了，此处有三个考点，分别为：

考点一：求解空间中的某向量 x 在基 A 下的坐标。

其实就是求解向量 x 在基 A 的各个“轴”上的投影。我们定义列向量 \(\lambda\) 为向量 x 在基 A 下的坐标，那么就有如下的表述：

\[ x = A \ \lambda \]

考点二：求解过度矩阵 P。

我们已知一个向量空间中的两个基分别为 A 和 B，若有矩阵 P 满足基变换公式：\(B = AP\)，我们就称 P 为从基 A 到基 B 的过渡矩阵

考点三：已知空间中的某向量 x 在基 A 下坐标为 \(\lambda\)，以及从基 A 到基 B 的过渡矩阵为 P，求解转换基为 B 之后的坐标 \(\gamma\)。

线性方程组的解的结构

本目是 3.3 目的一个知识补充，具体的线性方程组求解方法与 3.3 目几乎完全一致，只不过通过解的结构将解的结构进行了划分从而看似有些不同。但是殊途同归，都是一个东西。下面介绍本目与 3.3 目不同的地方：

我们从 3.3 目可以知道，无论是齐次线性方程组还是非齐次线性方程组，求解步骤都是：将系数矩阵（非齐次就是增广矩阵）进行行等价变换，然后对得到的方程组进行相对应未知变量的赋值即可。区别在于：

\[ \text{非齐次线性方程组的通解}=\text{非齐次线性方程组的一个特解}+\text{齐次线性方程组的通解} \]

解释：我们将

• 齐次线性方程组记为 \(Ax=0\)，解为 \(\eta\)，则有 \(A \eta = 0\)
• 非齐次线性方程组记为 \(Ax=b\)，假如其中的一个特解为 \(\eta^*\)，则 \(A\eta^*=b\)，假如此时我们又计算出了该方程组的其次线性解 \(\eta\)，则有 \(A\eta=0\)。那么显然有 \(A(\eta^*+\eta)=b\)，此时 \(\eta^* + \eta\) 就是该非齐次线性方程组的通解

也就是说本目对 3.3 目的线性方程组的求解给出了进一步的结构上的解释，即非齐次线性方程组的解的结构是基于本身的一个特解与齐次的通解之上的，仅此而已。当然了，本目在介绍齐次线性方程组解的结构时还引入了一个新的定理：若矩阵 \(A_{m\times n}\) 的秩为 \(r\), 则该矩阵的解空间的维度(基础解系中线性无关向量的个数)就是 \(n-r\)。即：

\[ dimS = n-r \]

该定理可以作为一些证明秩相等的证明题的切入点。若想要证明两个 $ n$ 元矩阵 \(A\) 和 \(B\) 的秩相等，可以转化为证明两个矩阵的基础解析的维度相等，即解空间相等。证明解空间相等进一步转向证明 \(Ax=0\) 与 \(Bx=0\) 同解，证明同解就很简单了，就是类似于证明一个充要条件，即证明 \(Ax=0 \to Bx=0\) 以及 \(Bx=0 \to Ax=0\)。