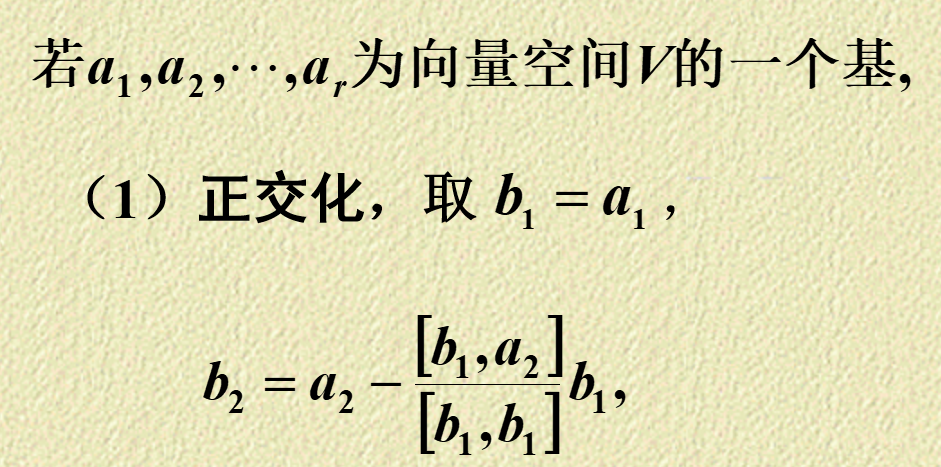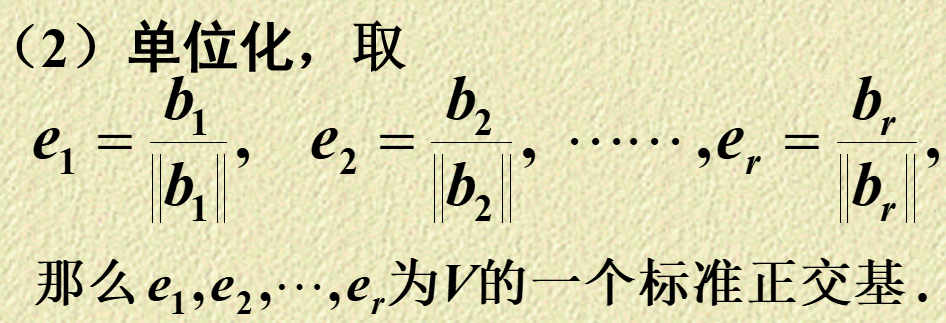跳转至

相似矩阵

5.1 正交矩阵与正交变换

正交向量。即两向量内积为 0，类似于二维平面中两个垂直的非零向量。

正交向量组。

  • 定义：向量组之间的任意两两向量均正交。
  • 性质：正交向量组一定线性无关。

标准正交基。

  • 定义：是某空间向量的基+正交向量组+每一个向量都是单位向量。

  • 求解方法：施密特正交化求解标准正交基。

施密特正交化求标准正交基 - 详细过程

一、正交化

正交化

正交化 - 续

二、单位化

单位化

正交矩阵。

  • 定义：满足 \(A^TA=E\ \text{or} \ AA^T=E\) 的方阵。
  • 定理：正交矩阵的充要条件为矩阵的行/列向量为单位向量且两两正交。

正交变换。

  • 定义：对于正交矩阵 \(A\)，\(y=Ax\) 称为称为正交变换。
  • 性质：\(||y||=\sqrt{y^Ty}=\sqrt{x^TA^TAx}=\sqrt{x^TEx}=\sqrt{x^Tx}=||x||\)，即向量经过正交变换之后长度保持不变。

5.2 特征值与特征向量

定义。对于一个 \(n\) 阶方阵 \(A\)，存在一个复数 \(\lambda\) 和一组 \(n\) 阶非零向量 \(x\) 使得 \(Ax =\lambda x\)，则称 \(x\) 为特征向量，\(\lambda\) 为特征值，\(|A-\lambda E|\) 为特征多项式。

特征值的性质。

  • \(n\) 阶矩阵 \(A\) 在复数范围内含有 \(n\) 个特征值，且：

    \[ \begin{aligned} \sum_{i = 1}^{n} \lambda _i =& \sum_{i = 1}^{n} a_{ii} \\ \prod_{i = 1}^{n} \lambda _i =& \left | A \right | \end{aligned} \]

  • 若 \(\lambda\) 是 \(A\) 的特征值，则 \(\phi{(\lambda)}\) 是 \(\phi{(A)}\) 的特征值。

特征向量的性质。对于同一个矩阵，不同的 特征值对应的特征向量之间是 线性无关 的。

5.3 相似矩阵

5.3.1 定义

对于两个 n 阶方阵 A, B 而言，若存在可逆矩阵 P 使得

\[ PAP^{-1}= B \]

则称 B 为 A 的相似矩阵，A 与 B 相似，也称对 A 进行相似变换，P 为相似变换矩阵

5.3.2 性质

若矩阵 A 与 B 相似，则 A 与 B 的特征多项式相同，则 A 与 B 的特征值也就相同，A 与 B 的行列式也就相同

5.3.3 矩阵多项式

一个矩阵 A 的多项式 \(\phi{(A)}\) 可以通过其相似矩阵 \(\Lambda\) 很轻松地计算出来为 \(P \phi{(\Lambda)} P^{-1}\)，即对角矩阵左乘一个可逆阵，右乘可逆阵的逆矩阵即可，而对角矩阵的幂运算就是对角元素的幂运算，故而非常方便就可以计算一个矩阵的多项式。那么计算的关键在于如何找到一个矩阵的相似矩阵？下面给出判定一个矩阵是否存在相似矩阵（可对角化）的判定定理：

n 阶方阵可对角化的充要条件为该方阵含有 n 个线性无关的特征向量

5.4 对称矩阵的对角化

本目讨论一个 n 阶方阵具备什么条件才能拥有 n 个线性无关的特征向量，从而可对角化。但是对于一般的方阵，情况过于复杂，此处只讨论 n 阶对称矩阵。即：一个 n 阶对角矩阵具备什么条件才能拥有 n 个线性无关的特征向量，从而可对角化。

答案是 n 阶对角矩阵一定是可对角化的。因为有一个定理是这样的：对于一个对称矩阵 A 而言，一定可以找到一个正交矩阵 P 使得 \(P^{-1}AP=\Lambda\)，又由于正交矩阵一定是可逆矩阵，因此一定可以找到矩阵 A 的 n 个线性无关的特征向量，从而 A 一定可对角化。

对称矩阵的性质如下：

  1. 对称矩阵的特征值均为实数
  2. 对称矩阵 A 的两个特征值 \(\lambda _1\) 与 \(\lambda _2\) 对应的两个特征向量分别为 \(P_1\) 和 \(P_2\)，若 \(\lambda_1 \ne \lambda_2\)，相比于一般的矩阵 \(P_1\) 与 \(P_2\) 线性无关，此时两者关系更强，即：\(P_1\) 与 \(P_2\) 正交
  3. 对称矩阵的每一个 k 重根，一定对应有 k 个线性无关的特征向量

因此本目相较于 5.3 目其实就是通过可对角化这一个概念，来告诉我们对称矩阵是一定可以求出对角矩阵的。而不用判断当前矩阵是否可对角化了。只不过在此基础之上还附加了一个小定理（也没给出证明），就是对称矩阵的相似变换矩阵一定是一个正交矩阵，那么也就复习回顾了 5.1 目中学到的正交矩阵的概念。为了求解出这个正交矩阵，我们需要在 5.3 目求解特征向量之后再加一个操作，即：对于一个 k 重根，根据上面的性质 3 我们知道当前的根一定有 k 个线性无关的特征向量，为了凑出最终的正交矩阵，我们需要对这 k 个线性无关的特征向量正交化。那么所有的特征值下的特征向量都正交化之后，又由性质 2 可知，不同的特征值下的特征向量又是正交的，于是最终的正交的相似变换矩阵也就求出来了，也就得到了对角矩阵 \(\Lambda\)。