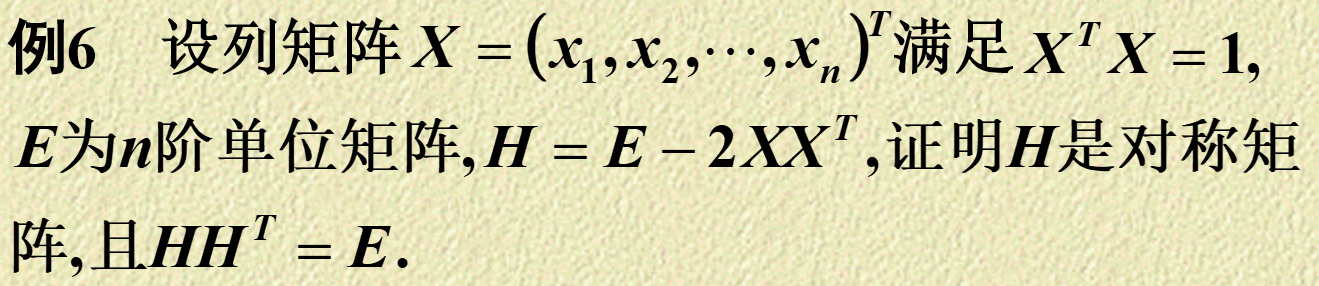矩阵

行列式是一种运算，运算结果是一个数，而矩阵是一种表示，表示一个数表，常用来表示一个线性方程组的系数。

基本概念¶

下面补充几个常见的名词：

方阵。若矩阵的行列数相等（假设为 \(n\)），则可以称该矩阵为：方阵、\(n\) 阶矩阵、\(n\) 阶方阵；
对角阵。即方阵的非主对角线元素均为 \(0\)，主对角线元素不限。符号表示为 \(\mathbf{\Lambda}=diag(\lambda_1,\lambda_2,\cdots,\lambda_n)\)；
单位阵。即方阵的非主对角线元素均为 \(0\)，主对角线元素均为 \(1\)。符号表示为 \(\mathbf{E}=diag(1,1,\cdots,1)\)；
纯量阵。即方阵的非主对角线元素均为 \(0\)，主对角线元素均为 \(\lambda\)。符号表示为 \(\mathbf{S}=diag(\lambda,\lambda,\cdots,\lambda)\)。

矩阵运算¶

元素级运算¶

两个形状相同的矩阵按元素逐个进行加、减、乘、除等运算。

向量级运算¶

向量有内积（点积）和外积（叉积）两种运算。前者计算出一个标量，后者计算出一个矩阵。以 \(\mathbf{x},\mathbf{y},\mathbf{z}\) 三个 \(n\) 维向量和实数 \(\lambda\) 为例：

向量的内积，记 \([\cdot,\cdot]\) 为两个长度相等的向量作内积，有以下性质：
1. \([\mathbf x, \mathbf y] = [\mathbf y,\mathbf x]\)；
2. \([\lambda \mathbf x,\mathbf y] = \lambda [\mathbf x,\mathbf y]\)；
3. \([\mathbf x + \mathbf y,\mathbf z] = [\mathbf x,\mathbf z] + [\mathbf y,\mathbf z]\)；
4. \([\mathbf x, \mathbf x] \geq 0\)，且当 \(x \ne 0\) 时有 \([\mathbf x,\mathbf x] > 0\)。
向量的长度，有以下性质：
1. 非负性：当 \(\mathbf x \ne \mathbf 0\) 时，\(\|\mathbf x\| > 0\)；当 \(\mathbf x =\mathbf 0\) 时，\(\|\mathbf x\| = 0\)；
2. 齐次性：\(\|\lambda\mathbf x\| = \lambda\|\mathbf x\|\)；
3. 三角不等式：\(\|\mathbf x +\mathbf y\| \le \|\mathbf x\| + \|\mathbf y\|\)。
向量的夹角：
1. 当 \(\|\mathbf x\| = 1\) 时，称 \(x\) 为单位向量；
2. 当 \(\|\mathbf x\| \ne \mathbf 0\land \|\mathbf y\| \ne \mathbf 0\) 时，\(\theta = \arccos \frac{[\mathbf x,\mathbf y]}{\|\mathbf x\|\|\mathbf y\|}\)。

矩阵级运算¶

矩阵算律如下：

结合律：\((\mathbf A\mathbf B)\mathbf C=\mathbf A(\mathbf B \mathbf C)\)；
分配率：\(\mathbf A(\mathbf B+\mathbf C)=\mathbf A\mathbf B+\mathbf A\mathbf C,(\mathbf B+\mathbf C)\mathbf A=\mathbf B\mathbf A+\mathbf C\mathbf A\)；
常数因子可以随意交换顺序：\(\lambda(\mathbf A\mathbf B)=(\lambda\mathbf A)\mathbf B=\mathbf A(\lambda\mathbf B)\)；
单位阵可以随意交换顺序或直接省略：\(\mathbf A\mathbf E=\mathbf E\mathbf A=\mathbf A\)；
幂运算：若 \(\mathbf A\) 是 \(n\) 阶矩阵，则 \(\mathbf A\) 的 \(k\) 次幂为 \(\mathbf A^k=\underbrace{\mathbf A\mathbf A\cdots \mathbf A}_{k\text{个}}\)，且 \(\mathbf A^m \mathbf A^k=\mathbf A^{m+k},(\mathbf A^m)^k=\mathbf A^{mk}\)，其中 \(m,k\) 为正整数。

*注：矩阵乘法没有交换律。\(\mathbf{AB}\) 称为 \(\mathbf{A}\) 左乘 \(\mathbf{B}\)。交换成立的前提是 \(\mathbf{A}\) 和 \(\mathbf{B}\) 左乘和右乘合法相等才可以。

矩阵转置¶

矩阵转置算律有以下四点：

\((\mathbf{A}^T)^T=\mathbf{A}\)；
\((\mathbf{A}+\mathbf{B})^T=\mathbf{A}^T+\mathbf{B}^T\)；
\((\lambda \mathbf{A})^T=\lambda \mathbf{A}^T\)；
\((\mathbf{AB})^T=\mathbf{B}^T\mathbf{A}^T\)。

证明 4：左边的 \(c_{ij}\) 其实应该是 \(AB\) 的 \(c_{ji}\) ，对应 \(A\) 的第 \(j\) 行与 \(B\) 的第 \(i\) 列，那么反过来对于 \(ij\) 就是 \(B\) 转置的第 \(i\) 行与 \(A\) 转置的第 \(j\) 列。

对称矩阵¶

对于一个方阵 \(\mathbf{A}\)，若有 \(\mathbf{A} = \mathbf{A}^T\) 则称 \(\mathbf{A}\) 为对称矩阵，简称对称阵。给一个对阵矩阵的例题：

方阵的行列式¶

行列式算律有以下三点：

\(\vert \mathbf{A}^T\vert=\vert \mathbf{A}\vert\)；
\(\vert \lambda \mathbf{A}\vert=\lambda^n\vert \mathbf{A}\vert\)；
\(\vert \mathbf{AB}\vert=\vert \mathbf{A}\vert\vert \mathbf{B}\vert\)。

对于上述第 3 点，显然有：\(\vert \mathbf{AB}\vert=\vert \mathbf{A}\vert\vert \mathbf{B}\vert=\vert \mathbf{B}\vert\vert \mathbf{A}\vert=\vert \mathbf{BA}\vert\)，即 \(\vert \mathbf{AB}\vert=\vert \mathbf{BA}\vert\)。

伴随矩阵¶

用 \(\mathbf{A}^*\) 表示 \(\mathbf{A}\) 的伴随矩阵，则有：

\[ \mathbf{AA}^* = \mathbf{A}^* \mathbf{A} = \vert \mathbf{A} \vert \mathbf{E} \]

其中 \(\mathbf{A}^*\) 表示为：

\[ \mathbf{A}^*= \begin{pmatrix} \mathbf{A}_{11} & \mathbf{A}_{21} & \cdots & \mathbf{A}_{n1}\\ \mathbf{A}_{12} & \mathbf{A}_{22} & \cdots & \mathbf{A}_{n2}\\ \cdots & \cdots & \cdots & \cdots\\ \mathbf{A}_{1n} & \mathbf{A}_{2n} & \cdots & \mathbf{A}_{nn}\\ \end{pmatrix} \]

其中 \(\mathbf A_{ij}\) 即代数余子式。

逆矩阵¶

逆矩阵的定义¶

对于 \(n\) 阶矩阵 \(\mathbf A\)，若有 \(\mathbf A\mathbf B = \mathbf B\mathbf A = \mathbf E\) ，则称 \(\mathbf B\) 为 \(\mathbf A\) 的逆矩阵，记作 \(\mathbf B=\mathbf A^{-1}\)。若 \(\vert\mathbf A\vert = 0\)，则 \(\mathbf A\) 为又称奇异矩阵；若 \(\vert\mathbf A\vert \ne 0\)，则 \(\mathbf A\) 为又称非奇异矩阵。

逆矩阵的性质¶

如下：

唯一性。如果矩阵 \(\mathbf A\) 可逆，则 \(\mathbf A\) 的逆矩阵是唯一的；
非奇异性。\(\mathbf A\) 可逆 \(\iff \vert\mathbf A \vert \ne 0\)。

逆矩阵的计算方法¶

知道了逆矩阵的定义和性质后，想要求解一个方阵的逆矩阵就有以下两种求法：

方法一：首先判断 \(\mathbf A\) 的行列式是否为 \(0\)，若 \(\vert\mathbf A\vert \ne 0\) ，则说明矩阵 \(\mathbf A\) 可逆，那么就有 \(\mathbf A^{-1} = \frac{1}{\vert\mathbf A\vert}\mathbf A^*\)；
方法二：如果可以找到 \(\mathbf A\mathbf B=\mathbf E\) 或 \(\mathbf B\mathbf A = \mathbf E\)，那么就有 \(\mathbf A^{-1}= \mathbf B\)。

逆矩阵的运算规律¶

如下：

\({(\mathbf A^{-1})}^{-1} = \mathbf A\)；
\(({\lambda \mathbf A})^{-1} = \frac{1}{\lambda} \mathbf A^{-1}\)；
\(({\mathbf A\mathbf B})^{-1} = \mathbf B^{-1}\mathbf A^{-1}\)；
\((\mathbf A^T)^{-1} = (\mathbf A^{-1})^{T}\)；
\(\vert \mathbf A^{-1}\vert = {\vert \mathbf A\vert}^{-1}\)；
\(\vert \mathbf A^*\vert = {\vert \mathbf A\vert}^{n - 1}\)。

克拉默法则¶

克拉默法则是求解一般线性方程组的一个特殊场景，适用于求解「未知数数量和方程个数相等，且系数行列式不为零」的线性方程组。

克拉默法则的定义¶

如果线性方程组：

\[ \begin{cases} a_{11}x_{1}+a_{12}x_{2}+&\cdots&+a_{1n}x_{n}= b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+&\cdots&+a_{2n}x_{n}= b_{2}\\ &\vdots&\\ a_{n1}x_{1}+a_{n2}x_{2}+&\cdots&+a_{nn}x_{n}= b_{n} \end{cases} \]

的系数矩阵 \(\mathbf A\) 的行列式不为零：

\[ \vert\mathbf A\vert =\begin{vmatrix}a_{11}&\cdots&a_{1n}\\\vdots&&\vdots\\a_{n1}&\cdots&a_{nn}\end{vmatrix}\neq0 \]

则方程组有唯一解：

\[ x_1 =\frac{\vert \mathbf A_1\vert}{\vert\mathbf A\vert}, x_2 =\frac{\vert \mathbf A_2\vert}{\vert\mathbf A\vert},\cdots, x_n =\frac{\vert\mathbf A_n\vert}{\mid \mathbf A\vert} \]

其中 \(\mathbf A_j\ (j=1,2,...,n)\) 是把系数矩阵 \(\mathbf A\) 中第 \(j\) 列的元素用常数向量 \(\mathbf b\) 代替后的 \(n\) 阶矩阵：

\[ \mathbf A_j = \begin{pmatrix} a_{11}&\cdots&a_{1, j-1}&b_1&a_{1, j+1}&\cdots&a_{1n}\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n1}&\cdots&a_{n, j-1}&b_n&a_{n, j+1}&\cdots&a_{nn} \end{pmatrix} \]

克拉默法则的证明¶

首先将方程组转化为矩阵方程：

\[ \mathbf A \mathbf x =\mathbf b,\vert \mathbf A\vert\ne 0 \]

然后应用逆矩阵消元：

\[ \mathbf x = \begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}= \mathbf A^{-1}\mathbf b = \frac{\mathbf A^*}{\vert\mathbf A\vert}\mathbf b = \frac{1}{\vert \mathbf A\vert} \begin{pmatrix} \mathbf A_{11}&\mathbf A_{21}&\cdots&\mathbf A_{n1}\\ \mathbf A_{12}&\mathbf A_{22}&\cdots&\mathbf A_{n2}\\ \vdots&\vdots&&\vdots\\ \mathbf A_{1n}&\mathbf A_{2n}&\cdots&\mathbf A_{nn} \end{pmatrix} \begin{pmatrix} b_1\\b_2\\ \vdots\\b_n \end{pmatrix} \]

最后应用行列式的按行/列展开中补充的性质即可得到最终的结果：

\[ \mathbf x = \cdots = \frac{1}{\mathbf \vert \mathbf A\vert} \begin{pmatrix} \mathbf A_{11}b_1+\mathbf A_{21}b_2+\cdots+\mathbf A_{n1}b_n\\ \mathbf A_{12}b_1+\mathbf A_{22}b_2+\cdots+\mathbf A_{n2}b_n\\ \vdots\\ \mathbf A_{1n}b_1+\mathbf A_{2n}b_2+\cdots+\mathbf A_{nn}b_n \end{pmatrix}= \frac{1}{\mathbf \vert \mathbf A\vert} \begin{pmatrix} {\mathbf \vert \mathbf A_1\vert}\\ {\mathbf \vert \mathbf A_2\vert}\\ \vdots\\ {\mathbf \vert \mathbf A_n\vert}\\ \end{pmatrix} \]

矩阵分块法¶

矩阵分块法本质就是将子矩阵看作一个整体进行运算，类似于分治算法。注意，在对矩阵进行分块计算的时候，有两个注意点，一是两个矩阵一开始的规格要相同，二是两个矩阵分块之后的子矩阵规格也要相同。我们重点关注对角分块矩阵。

对角分块矩阵的定义¶

主对角线为子矩阵：

\[ \mathbf A = \begin{pmatrix} \mathbf A_1 & & &\\ & \mathbf A_2 & &\\ & & \ddots &\\ & & & \mathbf A_s \end{pmatrix} \]

其中 \(\mathbf A_1,\mathbf A_2,...,\mathbf A_s\) 都是方阵。

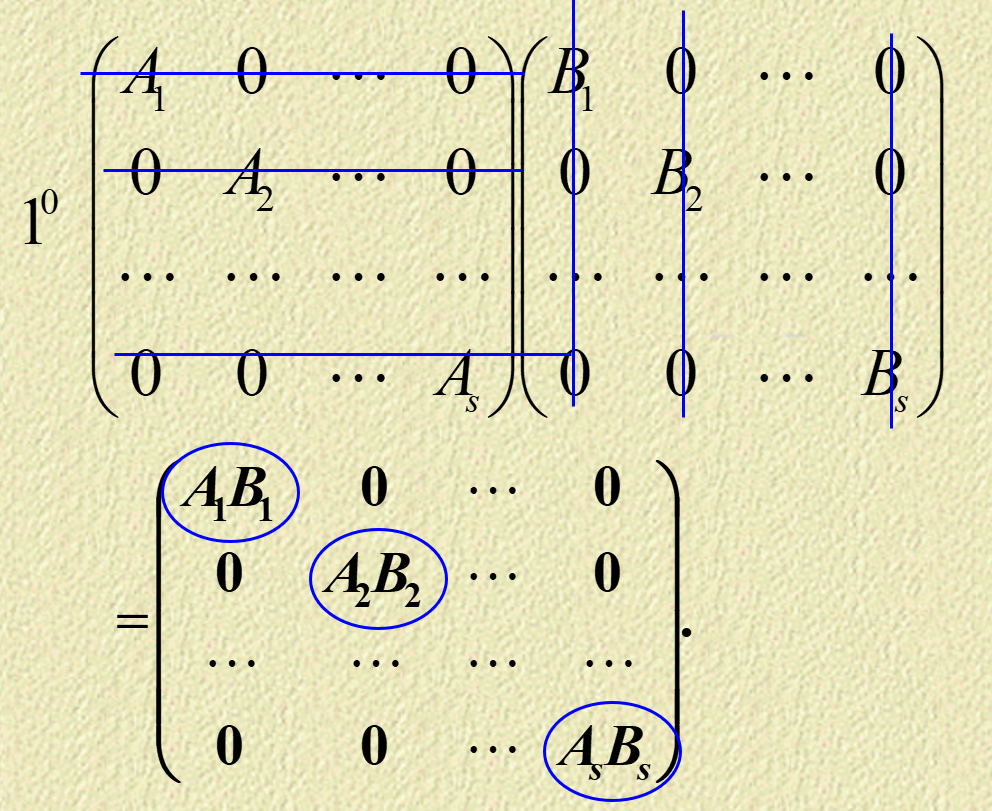
对角分块矩阵的运算¶

分别介绍幂运算、行列式运算、逆矩阵运算。

幂运算就是主对角线相应子矩阵的幂运算。如下图所示：

行列式运算使用了上三角的性质。如下式：

\[ \vert \mathbf A\vert = \vert \mathbf A_1\vert \vert \mathbf A_2\vert \cdots \vert \mathbf A_s\vert \]

逆矩阵就是主对角线的子矩阵按位取逆。若 \(\vert \mathbf A_i\vert\ne 0\ (i=1,2,\cdots,s)\)，则 \(\vert \mathbf A\vert\ne 0\)，且有：

\[ \mathbf A^{-1} = \begin{pmatrix} \mathbf A_1^{-1} & & &\\ & \mathbf A_2^{-1} & &\\ & & \ddots &\\ & & & \mathbf A_s^{-1} \end{pmatrix} \]