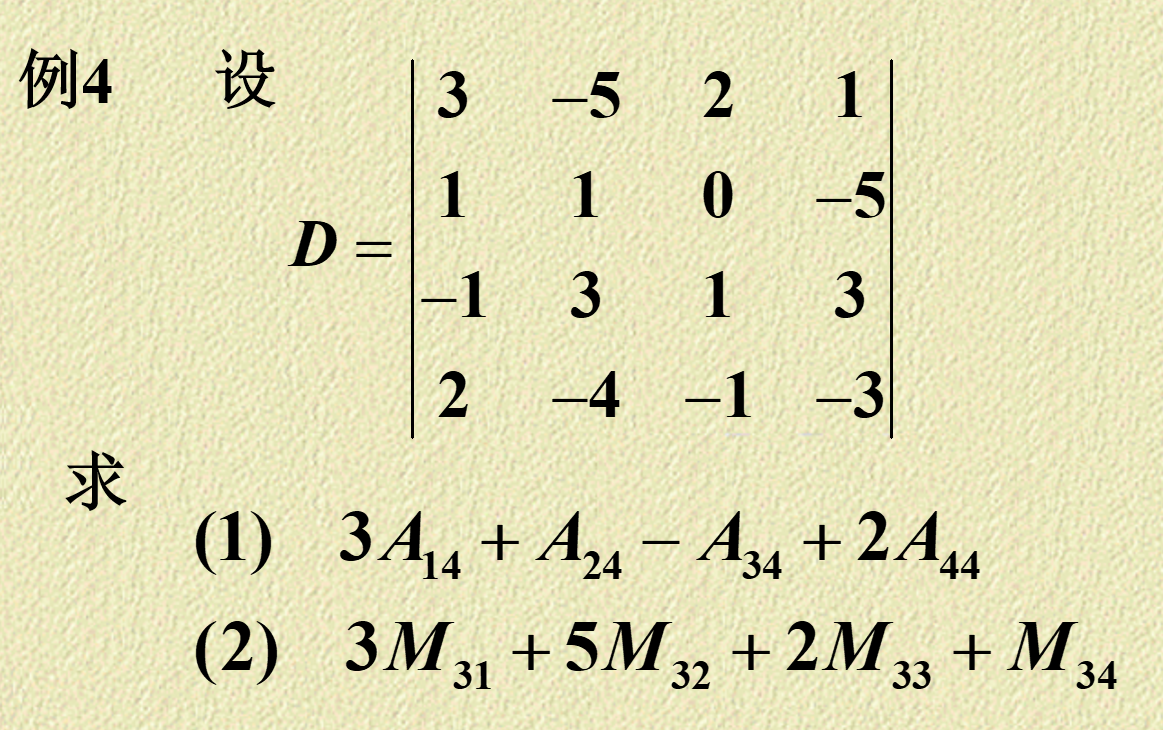行列式
国内的教材喜欢在一开始讲行列式 (Determinant),虽然笔者认为这其实和线代没什么关系,直接跳到 矩阵 开始学也行。
所谓行列式,其实就是一种运算,与 \(+\)、\(-\)、\(\times\)、\(\div\) 是一个东西,符号表示为 \(\vert \mathbf A\vert\)。其中 \(\mathbf A\) 为 \(n\times n\) 的数表,最终的运算结果是一个实数,即 \(\vert \mathbf A\vert\) 其实是一个实数。
基本概念¶
排列¶
若一个序列含有 \(n\) 个数并且序列中每一个位置只出现 \([1,n]\) 一次,则称该序列为全排列,简称排列;\([1,n]\) 的升序排列称为标准排列。
逆序数¶
即一个排列中每一个元素之前比其大的元素数量之和。可以用下面的代码来表示:
对换¶
即交换排列中的两个元素。有以下两个结论:
- 一个排列中两个元素对换,排列逆序数的奇偶性改变;
- 奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数。
行列式的定义与性质¶
行列式的定义¶
以 \(n\) 阶行列式为例,其值为 \(n!\) 个项之和。每一项的数值与符号定义为:
- 数值:每行选一个元素,每列选一个元素,行列各不相同;
- 符号:记 \(t(p_1p_2\cdots p_n)\) 为排列 \(p_1p_2\cdots p_n\) 的逆序数,那么符号为 \((-1)^{t(\text{行号})+N(\text{列号})}\)。
行列式的性质¶
行列式的性质可以用来简化求值,下面简单介绍一下 5 个常见的行列式性质及其推论(都可以用定义证出来,此处省略):
-
行列式与其转置行列式相等;
-
对换行列式的两个行或者列,行列式的符号改变;
- 推论:若行列式有两行或两列完全相同,则行列式的值为 \(0\)。
-
若行列式的某一行/列 \(\times k\),则行列式的值也 \(\times k\);
- 推论一:行列式的某一行/列中的公因子可以提到行列式之外;
- 推论二:若行列式有两行/列成比例,则行列式的值为零。
-
若行列式的某一行/列都是两数之和,则可以拆分成两个行列式之和;
-
把行列式的某一行/列乘一个常数累加到另一行/列上,行列式的值不变。
合理利用上述五个性质对行列式进行变换,就可以快速求解一个行列式。一般地,我们都会尽可能保证变换后的行列式左上角是数字 \(1\),从而配凑出「上三角行列式」,进而直接用主对角线之积求解。
行列式的按行/列展开¶
这里简单介绍一下行列式求值的另一个策略:按行/列展开。我们用 \(\mathbf{D}\) 表示行列式。用 \(\mathbf{M}_{ij}\) 表示余子式,即行列式去掉 \(\mathbf{D}_{ij}\) 元素所在的行和列后剩余元素拼接起来的行列式。用 \(\mathbf{A}_{ij}\) 表示代数余子式,其中 \(\mathbf{A}_{ij}=(-1)^{i+j}\mathbf{M}_{ij}\)。
若行列式的某一行/列只有一个元素不为零¶
则有:
证明:将某行/列唯一不为零的元素 \(a_{ij}\) 经过 \(i+j-2\) 次对换后整到 \(a_{11}\) 的位置后,剩余的 \(\mathbf{M}_{ij}\) 变换为下三角即可,即:
若行列式的某一行/列有多个元素不为零¶
则有:
证明:将展开的那一行/列通过加法原理进行拆分,然后利用上述只有一个元素不为零时的一般情况进行证明即可。
补充一个性质及其例题¶
已知 \(n\) 阶行列式 \(\mathbf{D}\),按第 \(x\) 行展开后有 \(\mathbf{D}=\sum_{i=1}^n a_{xi}\mathbf{A}_{xi}\),现在将 \(a_{xi}\) 替换为 \(a_{yi}\) 且 \(x\ne y\),则 \(\sum_{i=1}^n a_{yi}\mathbf{A}_{xi}=0\)。道理很简单,现在求解的值其实也是一个行列式,并且这个行列式有两行/列的元素完全相等,那么显然的行列式的值就是 \(0\)。
例如下面这道题:
显然 (1) 的结果为 \(0\);(2) 转化为 \(3\mathbf{A}_{31}-5\mathbf{A}_{32}+2\mathbf{A}_{33}-\mathbf{A}_{34}\) 后,与第一行做差然后通过余子式求解即可,结果为 \(-40\)。
特殊的行列式¶
下面补充几个特殊的行列式及其计算方法。
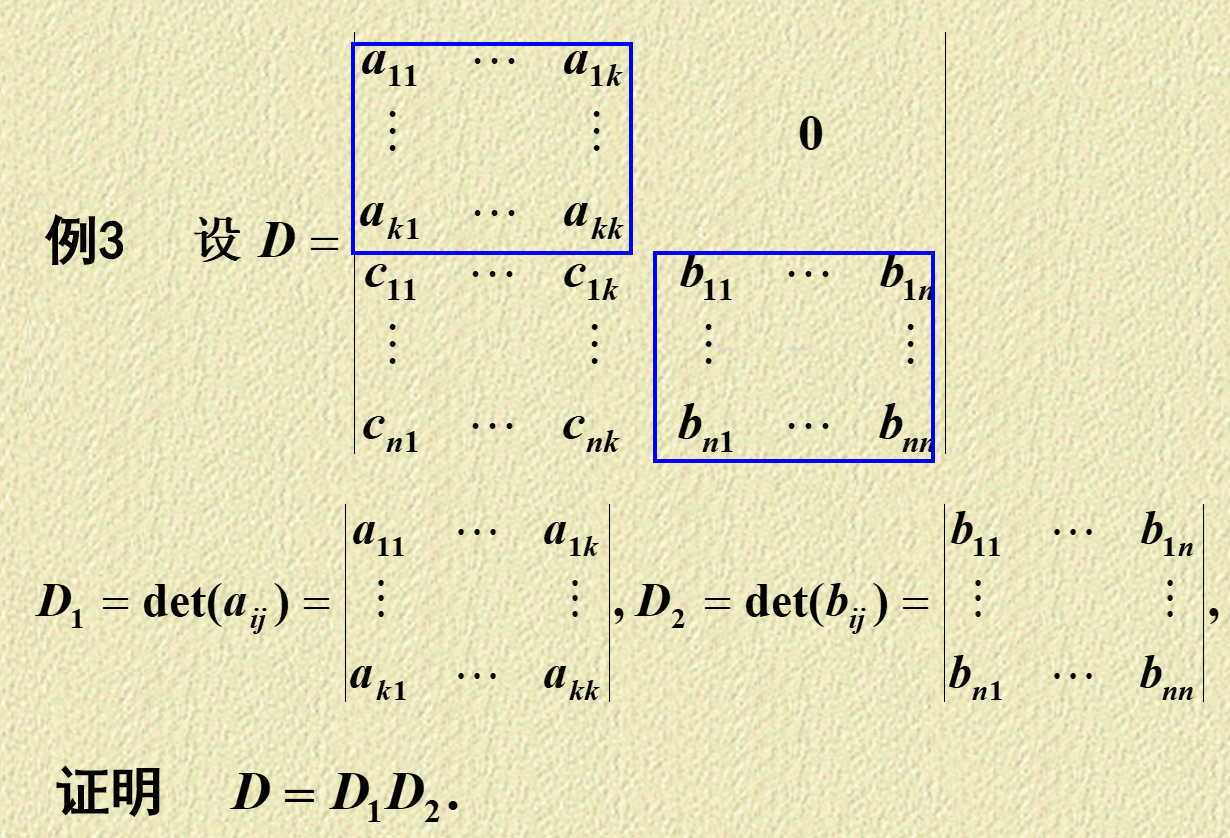
分块行列式¶
如下图所示:
计算方法:\(\mathbf{0}\) 在左下或右上就是左上角与右下角行列式之积 (\(\mathbf{D}=\mathbf{D}_1\mathbf{D}_2\)),\(\mathbf{0}\) 在左上或右下就是左下角与右上角行列式之积加上符号判定。
证明:将两个框选出来的区域转换为上三角即可。
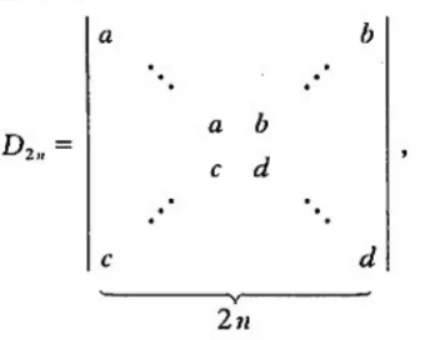
\(2n\) 阶行列式¶
如下图所示:
先行对换再列对换,通过分块行列式和数学归纳法,可得行列式的值是一个等比数列。
范德蒙德行列式¶
如下图所示:
证明。首先从最后一行开始,依次减去前一行的 \(x_1\) 倍,凑出第一列一个元素不为零的情况,最后通过数学归纳法即可求解。项数为 \(C_n^2\)。