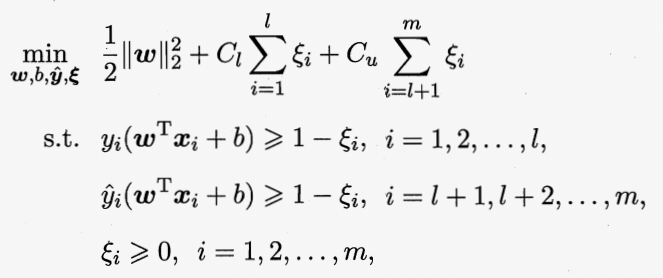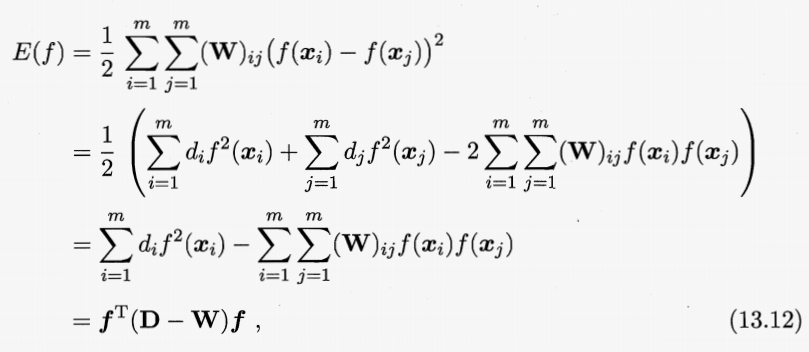半监督学习
半监督学习的根本目标:同时利用有标记和未标记样本的数据进行学习,提升模型泛化能力。主要分为三种:
- 主动学习
- 纯半监督学习
- 直推学习
未标记样本
对未标记数据的分布进行假设,两种假设:
- 簇状分布
- 流形分布
生成式方法
分别介绍「生成式方法」和「判别式方法」及其区别和联系。
生成式方法:核心思想就是用联合分布 \(p(x,y)\) 进行建模,即对特征分布 \(p(x)\) 进行建模,十分关心数据是怎么来(生成)的。生成式方法需要对数据的分布进行合理的假设,这通常需要计算类先验概率 \(p(y)\) 和特征条件概率 \(p(x\ |\ y)\),之后再在所有假设之上进行利用贝叶斯定理计算后验概率 \(p(y\ |\ x)\)。典型的例子如:
- 朴素贝叶斯
- 高斯混合聚类
- 马尔科夫模型
判别式方法:核心思想就是用条件分布 \(p(y\ |\ x)\) 进行建模,不对特征分布 \(p(x)\) 进行建模,完全不管数据是怎么来(生成)的。即直接学一个模型 \(p(y\ |\ x)\) 来对后续的输入进行预测。不需要对数据分布进行过多的假设。典型的例子如:
- 线性回归
- 逻辑回归
- 决策树
- 神经网络
- 支持向量机
- 条件随机场
自监督训练(补)
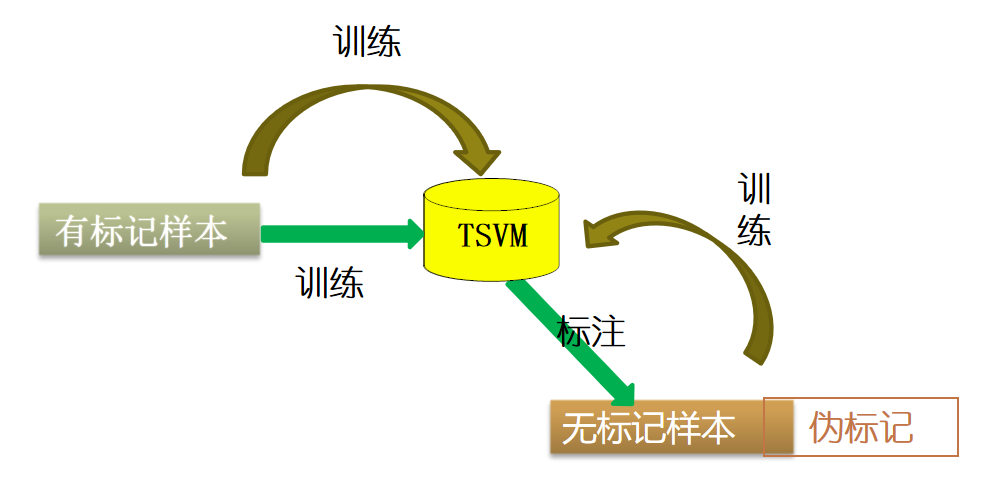
根本思想就是利用有标记数据进行模型训练,然后对未标记数据进行预测,选择置信度较高的一些样本加入训练集重新训练模型,不断迭代进行直到最终训练出来一个利用大量未标记数据训练出来的模型。
如何定义置信度高?我们利用信息熵的概念,即对于每一个测试样本都有一个预测向量,信息熵越大表明模型对其的预测结果越模糊,因此置信度高正比于信息熵小,将信息熵较小的测试样本打上「伪标记」加入训练集。
半监督 SVM
以经典 S3VM 中的经典算法 TSVM 为例。给出优化函数、算法图例、算法伪代码:
图半监督学习
同样解决分类问题,以「迭代式标记传播算法」为例。
二分类,可以直接求出闭式解。
算法逻辑。每一个样本对应图中的一个结点,两个结点会连上一个边,边权正比于两结点样本的相似性。最终根据图中已知的某些结点进行传播标记即可。与基于密度的聚类算法类似,区别在于此处不同的簇 cluster 可能会对应同一个类别 class。
如何进行连边?不会计算每一个样本的所有近邻,一般采用局部近邻选择连边的点,可以 k 近邻,也可以范围近邻。
优化函数。定义图矩阵的能量损失函数为图中每一个结点与所有结点的能量损失和,目标就是最小化能量损失和:
多分类,无法直接求出闭式解,只能进行迭代式计算。
新增变量。我们定义标记矩阵 F,其形状为 \((l+u) \times d\),学习该矩阵对应的值,最终每一个未标记样本 \(x_i\) 就是 \(\arg \max F_i\):