跳转至

集成学习

基本概念

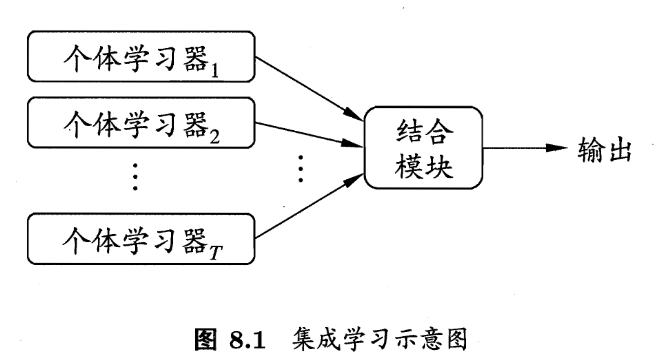
集成学习由多个不同的 组件学习器 组合而成。学习器不能太坏并且学习器之间需要有差异。如何产生并结合“好而不同”的个体学习器是集成学习研究的核心。集成学习示意图如下：

多个不同的学习组件

根据个体学习器的生成方式，目前集成学习可分为两类，代表作如下：

  1. 个体学习器直接存在强依赖关系，必须串行生成的序列化方法：Boosting；
  2. 个体学习器间不存在强依赖关系，可以同时生成的并行化方法：Bagging 和 随机森林 (Random Forest)。

Boosting 算法

Boosting 算法族的逻辑：

  1. 个体学习器之间存在强依赖关系；
  2. 串行生成每一个个体学习器；
  3. 每生成一个新的个体学习器都要调整样本分布。

以 AdaBoost 算法为例，问题式逐步深入算法实现：

  1. 如何计算最终集成的结果？利用加性模型 (additive model)，假定第 \(i\) 个学习器的输出为 \(h(x)\)，第 \(i\) 个学习器的权重为 \(\alpha_i\)，则集成输出 \(H(x)\) 为：

    \[ H(x) = \text{sign} \left(\sum_{i = 1}^T \alpha_i h_i(x)\right) \]

  2. 如何确定每一个学习器的权重 \(\alpha_i\) ？我们定义 \(\displaystyle \alpha_i=\frac{1}{2}\ln (\frac{1-\epsilon_i}{\epsilon_i})\)

  3. 如何调整样本分布？我们对样本进行赋权。学习第一个学习器时，所有的样本权重相等，后续学习时的样本权重变化规则取决于上一个学习器的分类情况。上一个分类正确的样本权重减小，上一个分类错误的样本权重增加，即：

    \[ D_{i+1}(x) = \frac{D_i(x)}{Z_i} \times \begin{cases} e^{-\alpha_i}&, h_i(x)= f(x) \\ e^{\alpha_i}&, h_i(x)\ne f(x) \end{cases} \]

代表算法：AdaBoost、GBDT、XGBoost。

Bagging 算法

在指定学习器个数 \(T\) 的情况下，并行训练 \(T\) 个相互之间没有依赖的基学习器。最著名的并行式集成学习策略是 Bagging。问题式逐步深入 Bagging 算法实现：

  1. 如何计算最终集成的结果？直接进行大数投票即可，注意每一个学习器都是等权重的
  2. 如何选择每一个训练器的训练样本？顾名思义，就是进行 \(T\) 次自助采样法
  3. 如何选择基学习器？往往采用决策树 or 神经网络

Random Forest 算法

随机森林 (Random Forest, RF) 是 Bagging 的一个扩展。问题式逐步深入随机森林算法实现：

  1. 如何计算最终集成的结果？直接进行大数投票即可，注意每一个学习器都是等权重的
  2. 为什么叫森林？每一个基学习器都是「单层」决策树
  3. 随机在哪？首先每一个学习器对应的训练样本都是随机的，其次每一个基学习器的属性都是随机的 \(k(k \in [1,V])\) 个（由于基学习器是决策树，并且属性是不完整的，故这些决策树都被称为弱决策树）

集成输出

基学习器有了，如何确定集成模型的最终输出呢？我们假设 \(T\) 个基学习器对于当前样本 \(x\) 的输出依次为 \(h_i(x),i=1,2,\cdots,T\)。模型的最终输出为 \(H(x)\)。

平均法

对于数值型输出 \(h_i(x) \in R\)，常见的结合策略采是 平均法。分为两种：

  1. 简单平均法：\(H(x) = \displaystyle \frac{1}{T} \sum_{i =1}^T h_i(x)\)
  2. 加权平均法：\(H(x) = \displaystyle\sum_{i=1}^T w_i h_i(x),\quad w_i \ge 0, \sum_{i=1}^Tw_i = 1\)

显然简单平均法是加权平均法的特殊。一般而言，当个体学习器性能差距较大时采用加权平均法，相近时采用简单平均法。

投票法

对于分类型输出 \(h_i(x) = [h_i^1(x), h_i^2(x), \cdots, h_i^N(x)]\)，即每一个基学习器都会输出一个 \(N\) 维的标记向量，其中只有一个打上了标记。常见的结合策略是 投票法。分为三种：

  1. 绝对多数投票法：选择超过半数的，如果没有则 拒绝投票
  2. 相对多数投票法：选择票数最多的，如果有多个相同票数的则随机取一个
  3. 加权投票法：每一个基学习器有一个权重，从而进行投票

学习法

其实就是将所有基学习器的输出作为训练数据，重新训练一个模型对输出结果进行预测。其中，基学习器称为“初级学习器”，输出映射学习器称为“次级学习器”或”元学习器” \(\text{(meta-learner)}\)。对于当前样本 \((x,y)\)，\(n\) 个基学习器的输出为 \(y_1 = h_1(x),y_2 = h_2(x),\cdots,y_n = h_n(x)\)，则最终输出 \(H(x)\) 为：

\[ H(x) = G(y_1, y_2, \cdots, y_n) \]

其中 \(G\) 就是次级学习器。关于次级学习器的学习算法，大约有以下几种：

  1. Stacking
  2. 多响应线性回归 (Mutil-response linear regression, MLR)
  3. 贝叶斯模型平均 (Bayes Model Averaging, BMA)

经过验证，Stacking 的泛化能力往往比 BMA 更优。

小结

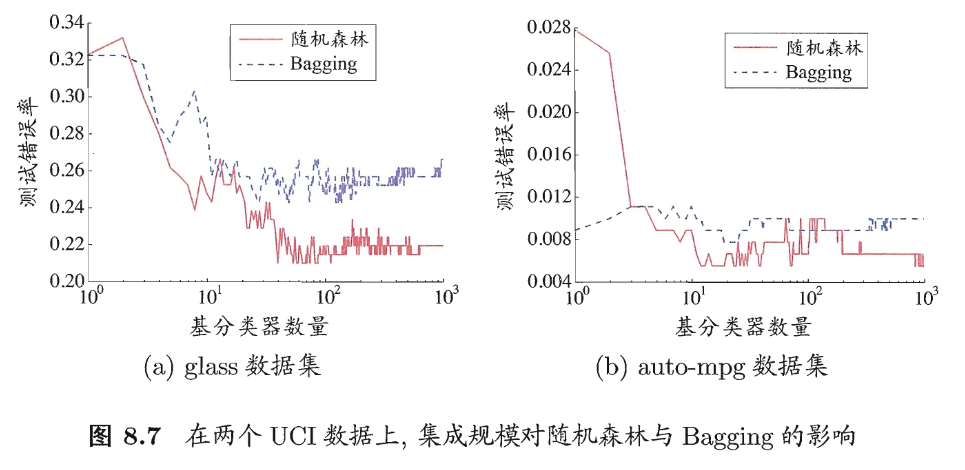
Random Forest 与 Bagging 相比，多增加了一个属性随机，进而提升了不同学习器之间的差异度，进而提升了模型性能，效果如下：

提升了模型性能

Random Forest 与 Bagging 均采用自助采样法。Bagging 优势在于不仅解决了训练样本不足的问题，同时 T 个学习器的训练样本之间是有交集的，这也就可以减小测试的方差。

区别：

  • 序列化基学习器最终的集成结果往往采用加权投票；
  • 并行化基学习器最终的集成结果往往采用平权投票。

联系：

  • 序列化减小偏差。即可以增加拟合性，降低欠拟合；
  • 并行化减小方差。即可以减少数据扰动带来的误差。