跳转至

聚类学习

本章我们学习一个经典的无监督学习方法：聚类。即通过某种规则将数据集划分为不同的簇。我们将会首先学习数据对象的距离计算规则，接着从结果论的角度学习如何评估一个聚类结果的好坏，最后按照类别介绍几个具体的聚类算法。

基本概念

距离计算。聚类的本质就是根据样本之间的距离将距离相近的数据对象认定为同一个类别，因此最关键的一步就是如何定义数据对象之间的距离（有些教材也会将距离度量成为邻近度度量）。无论是什么类型的属性，比如二元属性、标称属性、序数属性、数值属性等等，都可以归纳为以下两种距离计算的标准：

  1. 有序属性：闵可夫斯基距离；

  2. 无序属性：VDM 距离。

性能度量。一来是进行聚类算法的评估，二来也可以作为聚类算法的优化目标。分为两种，分别是外部指标和内部指标：

  1. 外部指标。所谓外部指标就是已经有一个“参考模型”存在了，将当前模型与参考模型的比对结果作为指标。我们考虑两两样本的聚类结果，定义下面的变量：

    \[ \begin{gathered} a=|SS|,SS=\{(\boldsymbol{x}_{i},\boldsymbol{x}_{j})\mid\lambda_{i}=\lambda_{j},\lambda_{i}^{*}=\lambda_{j}^{*},i<j)\},\\ b=|SD|,SD=\{(\boldsymbol{x}_{i},\boldsymbol{x}_{j})\mid\lambda_{i}=\lambda_{j},\lambda_{i}^{*}\neq\lambda_{j}^{*},i<j)\},\\ c=|DS|,DS=\{(\boldsymbol{x}_{i},\boldsymbol{x}_{j})\mid\lambda_{i}\neq\lambda_{j},\lambda_{i}^{*}=\lambda_{j}^{*},i<j)\},\\ d=|DD|,DD=\{(\boldsymbol{x}_i,\boldsymbol{x}_j)\mid\lambda_i\neq\lambda_j,\lambda_i^*\neq\lambda_j^*,i<j)\}, \end{gathered} \]

    显然 \(a+b+c+d=m(m-1)/2\)，常见的外部指标如下：

    • JC 指数：\(\displaystyle JC = \frac{a}{a+b+c}\)
    • FM 指数：\(\displaystyle \sqrt{\frac{a}{a+b} \cdot \frac{a}{a+c}}\)
    • RI 指数：\(\displaystyle \frac{2(a+d)}{m(m-1)}\)

    上述指数取值均在 \([0,1]\) 之间，且越大越好。

  2. 内部指标。所谓内部指标就是仅仅考虑当前模型的聚类结果。同样考虑两两样本的聚类结果，定义下面的变量：

    \[ \begin{aligned} \mathrm{avg}(C)&=\frac{2}{|C|(|C|-1)}\sum_{1\leqslant i<j\leqslant|C|}\operatorname{dist}(\boldsymbol{x}_{i},\boldsymbol{x}_{j}),\\ \mathrm{diam}(C)&=\max_{1\leqslant i<j\leqslant|C|}\mathrm{dist}(\boldsymbol{x}_{i},\boldsymbol{x}_{j}),\\ d_{\min}(C_i,C_j)&=\min_{\boldsymbol{x}_i\in C_i,\boldsymbol{x}_j\in C_j}\mathrm{dist}(\boldsymbol{x}_i,\boldsymbol{x}_j),\\ d_{\mathrm{cen}}(C_i,C_j)&=\mathrm{dist}(\boldsymbol{\mu}_i,\boldsymbol{\mu}_j), \end{aligned} \]

    常见的内部指标比如：轮廓系数。

基于划分的聚类算法

Kmeans 及其变种都只适用于 凸形状 的样本分布。

K-means

目标函数（损失函数）定义为：

\[ \text{loss}=\sum_i^K\sum_{x\in c_i}\|x-c_i\|_2^2 \]

Kmeans 算法流程大体上可以归纳为三步：

  1. 随机选择 k 个数据对象作为 \(k\) 个聚类中心（K 均值算法需要提前给出超参数，即簇的数量 \(k\)）；
  2. 枚举所有样本并将其划分到欧氏距离（或其他距离度量方法）最近的一个聚类中心；
  3. 更新 \(k\) 个簇中心为簇中所有样本的均值。

重复上述迭代过程直到算法收敛。达到以下任意一种条件即表示算法收敛：

  • 损失函数小于阈值；
  • 达到最大迭代次数。

假设样本数量为 N，簇的数量为 K，最大迭代轮数为 iter，则 Kmeans 算法的时间复杂度为 \(O(\text{iter} \times NK)\)。

K-means++

此法相对于 K-means 做出了一个小的改进。在一开始选择 k 个聚类中心时，并不是随机初始化 k 个，而是首先随机出 1 个，然后循环 \(k-1\) 次选择剩下的 k-1 个聚类中心。选择的规则是：每次选择最不可能成为新的聚类中心的数据对象，或者是到所有聚类中心的最小距离最大的数据对象。

Bisecting K-means

此法叫做二分 K-means 算法。具体的，在一开始将所有的数据对象划分为一个簇，然后每次选择一个误差最大的簇进行二分裂，不断分裂直到收敛。这种方法不能使得 Loss 最小，但是可以作为 K-means 算法的一个预热，比如可以通过这种方法得到一个相对合理的簇中心，然后再利用 K-means 算法进行聚类。

K-mediods

目标函数定义为：

\[ \text{loss}=\sum_i^K\sum_{x\in o_i}\lvert x-o_i\rvert \]

即 K 中心点算法。例如 PAM 算法，其使用实际的数据对象作为簇中心而不是用均值众数等新点作为簇中心。具体的，对于每一个簇中心 \(O_i\)，随机选择一个非簇中心的数据对象 \(O_{\text{random}}\)，如果用 \(O_{\text{random}}\) 替换 \(O_i\) 之后损失减小，则替换，否则继续迭代直到算法收敛。

基于层次的聚类算法

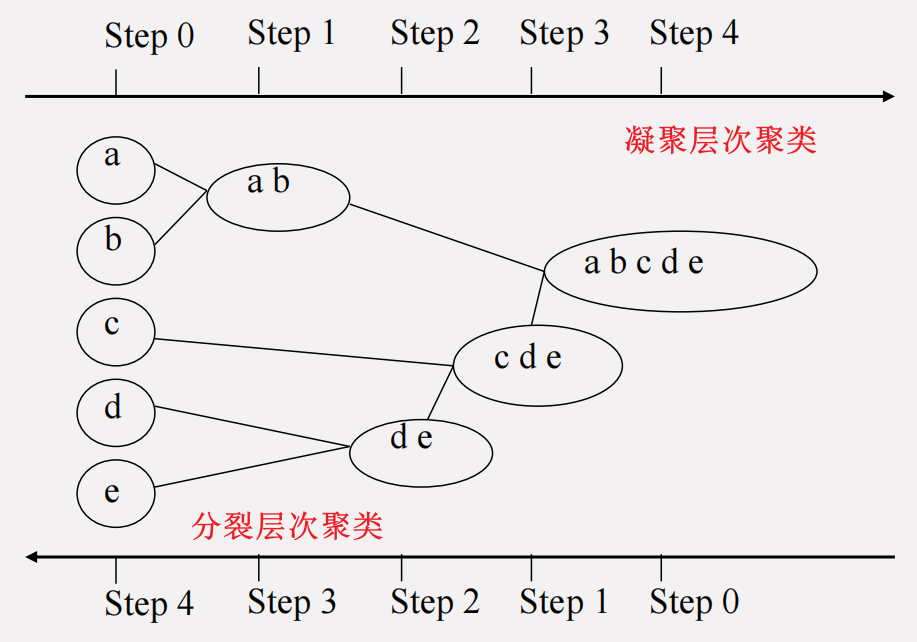
主要介绍簇之间的邻近性度量方法以及凝聚方法 (Agglomerative, AGNES) 和分裂方法 (Divisive Analysis, DIANA)。两种算法可以形象的表述为下图：

凝聚层次聚类 vs 分裂层次聚类

簇之间的邻近性度量

单链（Single-linkage）：簇之间的邻近度定义为不同簇中两个最近的数据对象的距离；

全链（Complete-linkage）：簇之间的邻近度定义为不同簇中两个最远的数据对象的距离；

均链（Average-linkage）：簇之间的邻近度定义为不同簇中所有数据对象之间距离的均值；

质心距离（Distance between centroids）：簇之间的邻近度定义为不同簇的质心之间的距离。

AGNES

凝聚算法有点类似于并查集，初始时每一个样本点都是一个簇，不断合并最接近的两个簇直到达到需要的簇数量就停止合并。而这里簇之间的距离就按照上面介绍的簇之间的邻近性度量来实现。

不同邻近度方法下凝聚层次聚类对比：

单链 全链 均链 质心距离
优点 可以处理非椭圆形的簇 簇间的距离不易受到噪声或异常值的影响 簇间的距离不易受到噪声或异常值的影响
缺点 聚类结果对噪声或异常值敏感 倾向于分裂较大的簇 倾向于形成球形的簇 倾向于形成球形的簇

DIANA

分裂算法有点类似于 Bisecting K-means，每次选一个簇根据某种规则将其分类为两个簇，直到达到需要的簇数量就停止分裂。

基于密度的聚类算法

DBSCAN

基于密度的带噪声空间聚类（Density-Based Spatial Clustering of Application with Noise, DBSCAN）

其实，就是一个朴素 dfs。算法定义为：

  • 每次随机选择一个没有访问过的对象开始 dfs；
  • 如果发现无法成为核心对象，即邻域 \(\epsilon\) 内的数据对象数量小于 \(\text{Minpts}\)，则标记为 visited 并重新选点；
  • 如果可以成为核心对象，则形成一个簇 C 并将当前邻域内没有归属的数据对象全都纳为 C 的数据对象，并以这些新纳入的数据对象为起点递归的拓展，直到无法拓展新的数据对象。

基于密度的 DBDSAN 聚类算法可以适应更加复杂的数据分布场景，但是缺点在于对超参数 (\(\epsilon,\text{Minpts}\)) 很敏感。并且由于超参数是二维联合的，因此如何调参 (\(\epsilon,\text{Minpts}\)) 是一个很困难的事。在此基础之上，提出 DBSCAN 算法的团队又提出了其改良版本：OPTICS 算法。

OPTICS

用于确定聚类结构的排序点聚类（Ordering Points To Identify the Clustering Structure, OPTICS）

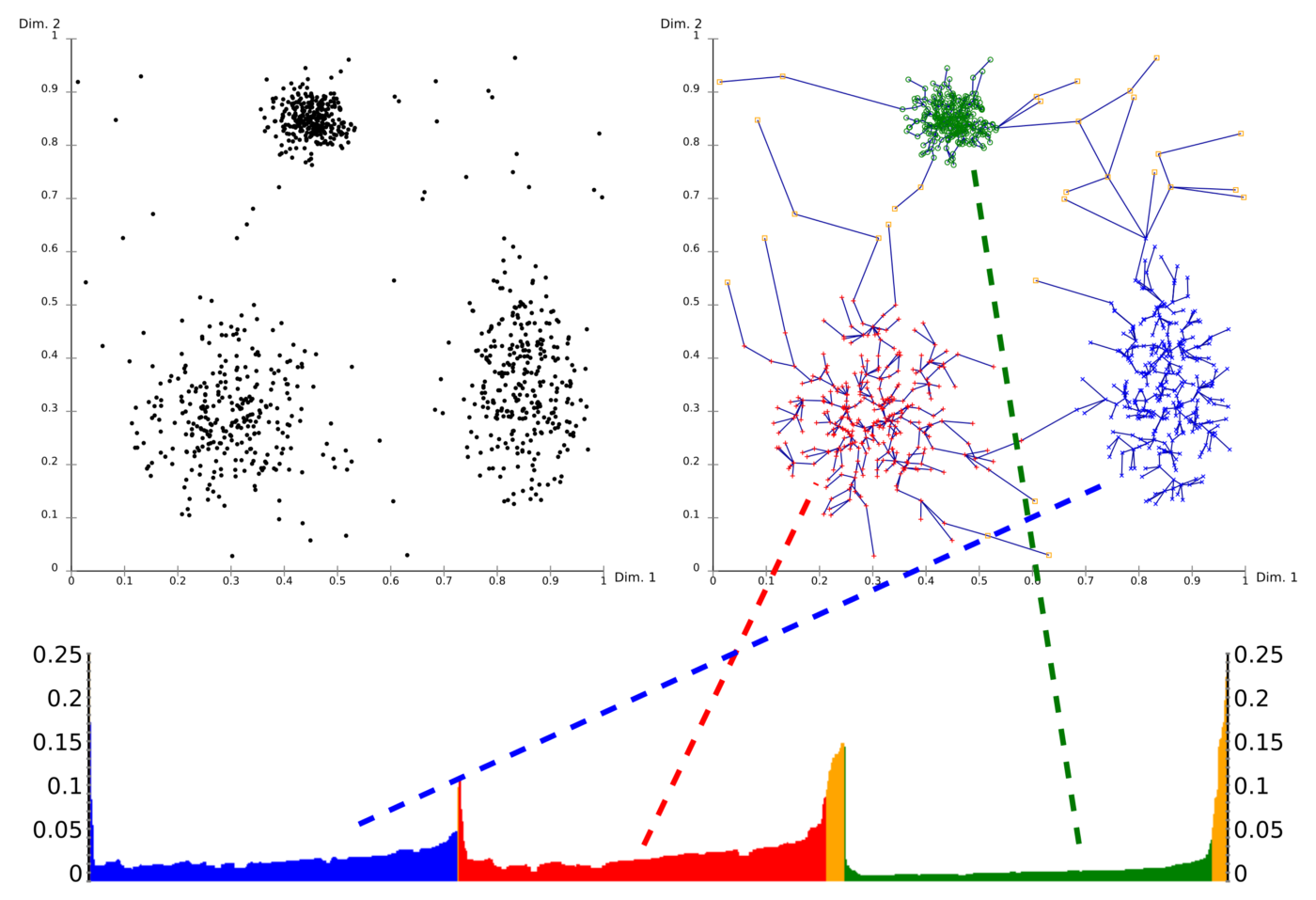
基于密度的 OPTICS 算法延续了 DBSCAN 的策略，只需要提前设定邻域内最少数据对象数量 Minpts 而不需要提前设置邻域大小 \(\epsilon\)。有两个关键的概念定义：

  • 核心距离：数据对象成为核心对象的最小半径阈值；

  • 可达距离：对于两个数据对象 p 和 q，其中 q 是核心对象，可达距离定义为：

    \[ \max{(q \text{ 的核心距离}, p \text{ 与 } q \text{ 的距离})} \]

最终可以得到一个按照某种规则排序的以及其可达距离。此时可以自行划分邻域的值进而按照预期进行聚类而不会像 DBSCAN 一样不受控制。OPTICS 的演示效果如下所示：

OPTICS 算法演示