评估
模型在训练(学习、拟合)的过程中,必须要有一个目标,比如最小化目标函数或最大化目标函数,这里的目标函数都可以转化为损失函数,因此下文这两个概念不做区分。
而目标函数不光可以用来训练模型,也可以评估模型。因此我们以评估模型为引,详细展开各个学习任务中常用的目标函数以及评估指标。最后简单介绍一下模型损失的来源以及超参调优的策略。
回归任务
对于回归任务,模型输出的是一个具体的实数。常见的度量指标如下。
均方误差 (Mean Square Error, MSE)。即模型预测值 \(f(\boldsymbol{x}_i)\) 与标签值 \(y_i\) 的平均平方误差,也就是所谓的方差。取值范围为 \([0,+\infty]\),越小越好。如下式:
\(R^2\) 分数。取值范围为 \([-\infty,1]\),越大越好。如下式:
二分类任务
对于二分类任务,模型输出的大多都是样本属于正例的概率。常见的度量指标如下。
混淆矩阵 (confusion matrix)。二分类模型的预测结果。
表 1. 二分类结果混淆矩阵
| 真实情况 \ 预测结果 | 正例 | 反例 |
|---|---|---|
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假反例) | TN(真反例) |
基于上述混淆矩阵 ,我们定义以下度量指标:
表 2. 二分类度量指标(数据平衡时)
| 名称 | 公式 | 备注 |
|---|---|---|
| 准确率 (Accuracy) | \(\text{Accuracy}=\dfrac{TP+TN}{TP+FN+FP+TN}\) | 错误率 = 1 - 准确率 |
| 查准率/精度 (Precision) | \(P = \dfrac{TP}{TP+FP}\) | 该指标可以理解为「我认为的正例里面确实为正例的样本数量越多越好」。适用于商品搜索推荐,即在有限的屏幕内容中显示出尽可能多的用户偏好商品。 |
| 查全率/召回率 (Recall) | \(R = \dfrac{TP}{TP+FN}\) | 该指标可以理解为「在测试集的所有正例里面预测为正例的样本数量越多越好」。适用于逃犯、病例检测,需要尽可能将正例检测出来。 |
当训练集正负例「不平衡」时,需要按照正负例分开评估。如下:
表 3. 二分类度量指标(数据不平衡时)
| 名称 | 公式 | 备注 |
|---|---|---|
| 敏感性 (Sensitivity) | \(\text{Sensitivity} = \dfrac{TP}{TP + FN}\) | 该指标只评估模型对正例的预测准确性。 |
| 特异性 (Specificity) | \(\text{Specificity} = \dfrac{TN}{FP + TN}\) | 该指标只评估模型对负例的预测准确性。 |
由于实际场景中需要「兼顾查准率和查全率」同时可能需要对其中一个有所偏好,我们引入 \(F_{\beta}\) 分数。当 \(\beta=1\) 时就是标准的 F1 分数,当 \(\beta>1\) 时对查全率有偏好,当 \(\beta<1\) 时对查准率有偏好。\(F_{\beta}\) 分数如下式:
上述指标都是针对一个混淆矩阵展开,如果需要度量「二分类模型的泛化能力」是远远不够的。为此我们引入 P-R 曲线和 ROC 曲线。两者的产生方式相同,都是:根据二分类模型对测试数据类别的预测概率划分一个阈值,并将预测概率超过阈值的判定为正例,低于阈值的判定为负例。然后将阈值依次选择为每个样本(假设为 \(N\) 个测试样本)的预测概率值进行二分类即可得到 \(N\) 个混淆矩阵,进而得到曲线中的 \(N\) 个数据点。
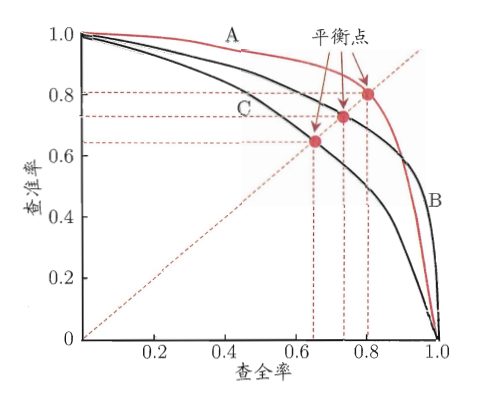
P-R 曲线。横坐标为查全率 (Recall),纵坐标为查准率 (Precision)。
图 1. P-R 曲线
-
趋势解读。随着正例判定阈值不断下降,很显然查全率 \(R\) 会不断上升,查准率 \(P\) 会不断下降;
-
曲线解读。不同曲线对应了不同模型的泛化能力,我们用「P-R 曲线与横纵坐标围成的面积」来衡量模型的泛化能力,面积越大则对应模型的泛化性能更好。因此上图中 A 模型泛化能力比 C 模型要好。但是我们往往会遇到比较 \(A\) 与 \(B\) 两个模型泛化能力的情况,考虑到计算实际曲线面积的复杂性,引入「平衡点」概念。平衡点就是 \(P=R\) 这条直线与 P-R 曲线的交点。平衡点越高,则对应的模型泛化能力越好。因此上图中 \(A\) 模型的性能优于 \(B\) 模型的性能。
ROC (Receiver Operating Characteristic, ROC) 曲线。即受试者工作特征曲线。横坐标为假正例率 \(\displaystyle FPR = \frac{FP}{FP+TN}\),纵坐标为真正例率 \(\displaystyle TPR = \frac{TP}{TP+FN}\)。
图 2. ROC 曲线图与 AUC
-
趋势解读。随着正例判定阈值不断下降,真正例率与假正例率均会不断上升;
-
曲线解读。不同曲线同样对应了不同模型的泛化能力。我们用「ROC 曲线下方的面积 (Area Under ROC Curve, AUC)」来衡量模型的泛化能力,面积越大则对应模型的泛化性能越好。取值范围为 \([0.5,1]\),其中 \(0.5\) 表示模型进行随机预测的性能。
多分类任务
我们可以将多分类问题拆分为多个二分类问题(假设为 \(n\) 个),从而可以获得多个混淆矩阵。根据求平均顺序的不同,多分类任务的度量指标分为「宏」与「微」两个类别。其中宏是先求指标再取平均,微是先取平均再求指标。
表 4. 多分类任务度量指标表
| 类别 \ 指标 | 查准率 | 查全率 | F1 分数 |
|---|---|---|---|
| 宏 | \(\displaystyle\text{macroP} = \frac{1}{n} \sum_{i=1}^n P_i\) | \(\displaystyle \text{macroR} = \frac{1}{n} \sum_{i=1}^n R_i\) | \(\displaystyle\text{macroF}_1 = \frac{2 \cdot\text{macroP} \cdot\text{macroR}}{\text{macroP}+\text{macroR}}\) |
| 微 | \(\displaystyle\text{microP} = \frac{\overline{TP}}{\overline{TP}+\overline{FP}}\) | \(\displaystyle\text{microR} = \frac{\overline{TP}}{\overline{TP}+\overline{FN}}\) | \(\displaystyle\text{microF}_1 = \frac{2 \cdot \text{microP} \cdot \text {microR}}{\text{microP}+\text{microR}}\) |
模型误差
误差类别
知道了数据集的划分策略后,针对不同的数据,模型会对应不同的误差。有以下四种:
- 训练误差。针对训练数据而言,即模型在训练集上的预测错误率。训练轮数越多或模型的复杂度越高,训练误差越小;
- 验证误差。针对验证数据而言,即模型在验证集上的预测错误率;
- 测试误差。针对测试数据而言,即模型在测试集上的预测错误率;
- 泛化误差。针对测试数据而言,即模型在多个测试集上「测试误差的期望」。
一般来说,训练误差 \(<\) 验证误差 \(\approx\) 测试误差 \(\approx\) 泛化误差。
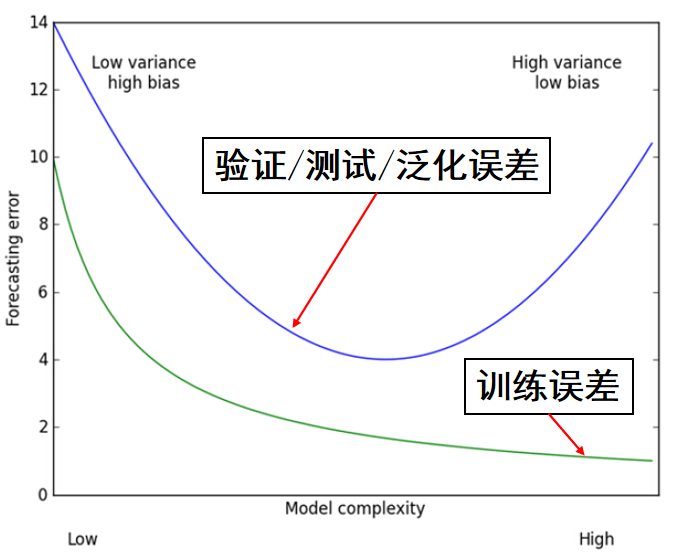
图 3. 训练误差与测试误差随模型复杂度的变化趋势图
可以看到,模型复杂度不够就会欠拟合导致测试误差较高,模型复杂度过高就会过拟合也会导致测试误差较高。
误差规避
为了避免模型发生欠拟合或过拟合,我们需要对模型做出一些约束或者设置一些训练策略。
欠拟合解决方法。欠拟合就说明模型复杂度不够,我们需要增加模型的复杂度,常见的规避欠拟合的方法如下:
-
决策树:增加树的深度;
-
神经网络:增加训练轮数。
过拟合解决方法。与欠拟合相对,常见的规避过拟合的方法如下:
- 早停法 (Early Stopping)。当发现有过拟合现象就停止训练。代码实现上可以体现为取最佳模型为验证误差最小时的模型;
- 增加惩罚 (Penalizing Large Weight)。在经验风险上加一个「正则化」项;
- 集成学习思想。用多个弱分类器投票产生结果从而降低模型偏差;
- 剔除部分神经元 (Dropconnection)。在神经网络的全连接层中剔除部分神经元,即让部分神经元存储的值为 \(0\)。
正则化。我们有必要先理清楚正则化项都有哪些以及对应的数学表达式是什么。如下表:
表 5. 正则化项表
| 机器学习中的称呼 | 实际名称 | 数学表达式 |
|---|---|---|
| 一般式 | \(p\) 范数的 \(k\) 次方 | \(\displaystyle \|\boldsymbol{x}\|_p^k = \left ( \left ( \sum_{i = 1}^{N}\vert x_i \vert^{p} \right)^{1/p} \right)^k\) |
| \(L_1\) 正则化项 | \(1\) 范数 | \(\displaystyle \|\boldsymbol{x}\|_1 = \sum_{i = 1}^N \vert x_i \vert\) |
| \(L_2\) 正则化项 | \(1\) 范数的平方 | \(\displaystyle \|\boldsymbol{x}\|_2^2 = \left ( \left ( \sum_{i = 1}^{N}\vert x_i \vert^{2} \right)^{1/2} \right)^2 = \sum_{i = 1}^{N}\vert x_i \vert^{2} = \sum_{i = 1}^{N}x_i^{2}\) |
| 默认的范数 | \(2\) 范数 | \(\displaystyle \|\boldsymbol{x}\| = \left (\sum_{i = 1}^{N}\vert x_i \vert^{2} \right)^{1/2}\) |
通过给目标函数添加正则化项,不仅可以防止过拟合,其中的 \(L_1\) 正则化项还可以进行特征选择,因为其使得不重要特征的系数被惩罚得很小,通过特征选择也可以降低计算量从而提升计算效率。
然而给目标函数添加正则化项并非万金油选项。在整个目标函数中正则化项有着举足轻重的意义,一旦正则化项的系数发生了微小的变动,对于整个模型的影响都是巨大的。因此有时添加正则化项并不一定能带来泛化性能的提升。
误差来源
如何从理论上来解释模型的泛化误差呢?我们引入「偏差方差分解」理论。
在此之前我们需要知道偏差、方差和噪声的基本定义:
- 偏差:学习算法的期望输出与真实结果的偏离程度。刻画模型本身的拟合能力;
- 方差:使用同规模的不同训练集进行训练时给模型带来的性能变化。刻画数据扰动给模型带来的影响;
- 噪声:当前任务上任何算法所能达到的期望泛化误差的下界。刻画问题本身的难度。
偏差方差分解。我们尝试对泛化误差的组成进行分解。先进行以下的符号定义:\(x\) 为测试样本,\(y_D\) 为 \(x\) 在数据集中的标签,\(y\) 为 \(x\) 的真实标签,\(f(x;D)\) 为模型在训练集 \(D\) 上学习后的预测输出,\(E(f; D)\) 为模型的泛化误差。以回归任务为例,有以下的变量定义:(\(\mathbb{E}\) 表示期望)
- 模型在测试样本上的期望输出:\(\overline{f}(x) = \mathbb{E}_D[f(x;D)]\)
- 使用相同规模训练集训练出来的不同模型在测试样本上的预测方差:\(var(x) = \mathbb{E}_D[(\overline{f}(x) - f(x;D))^2]\)
- 模型的期望输出与真实标记的偏差:\(bias^2(x) = (\overline{f}(x) - y)^2\)
- 噪声:\(\epsilon ^2 = \mathbb{E}_D[(y_D - y)^2]\)
经过简单的推导就可以得到偏差方差分解的结论:
即模型的泛化误差由偏差、方差和噪声三部分组成。那么模型的泛化性能也就是由学习算法的能力(偏差)、数据的充分性(方差)以及学习任务本身的难度(噪声)共同决定的。因此给定一个学习任务,我们可以从偏差、方差和噪声三个角度优化模型:
- 使偏差尽可能小:选择合适的学习算法充分拟合数据;
- 使方差尽可能小:提升模型的抗干扰能力来减小数据扰动产生的影响;
- 使噪声尽可能小:选择合适的数据增强方法来减小因为数据本身带来的误差。
偏差方差窘境。其实偏差和方差是有冲突的,这被称为偏差方差窘境(bias-variance dilemma)。对于给定的学习任务:
- 模型一开始拟合能力较差,对于不同的训练数据不够敏感,此时泛化误差主要来自偏差;
- 随着训练的不断进行,模型的拟合能力逐渐增强,这会加剧模型对数据的敏感度,从而使得方差主导了泛化误差;
- 在模型过度训练后,数据的轻微扰动都可能导致预测输出发生显著的变化,此时方差就几乎完全主导了泛化误差。
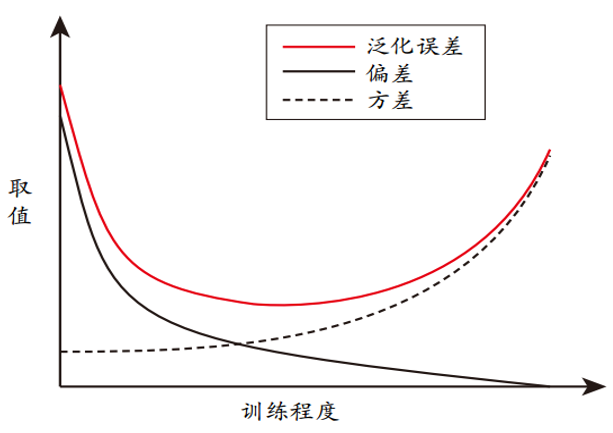
图 4. 泛化误差与偏差、方差的关系示意图
超参调优
所谓的调参,是基于超参数进行的。我们知道一个模型有「可训练」的参数和「不可训练」的超参数,调参调的就是这里的超参数。在将数据集划分为训练集、验证集和测试集的情况下,一般使用训练集学习可训练的参数,使用验证集来度量不同超参数组合下的模型性能,得到最佳的超参数组合后才能最终使用测试集进行测试。
常见的 超参调优方法 有:网格搜索、随机搜索、贝叶斯优化。