异常检测

异常检测也可以称为离群点检测，主要用来检测出离群点。但是这里的异常检测和 chapter2.1 数据清理并非一回事。

在非异常检测的任务中，通常将噪声和离群点当做一个东西来处理掉；
而在异常检测的任务中，需要对两者进行区分，并且异常检测的任务就是检测出离群点。

因为离群点的出现可能预示着数据中含有不同的分布情况，这通常是让人感兴趣的，而噪声无论是什么任务都需要提前处理掉。

基本概念

在异常检测任务中，数据往往都没有进行标注；并且由于异常数据的比例极少，这也导致了数据不平衡的问题；与此同时，由于异常数据的特征是没有定义的，很容易就将其和噪声混淆了。

由于上述的种种限制，使得异常检测任务很难使用二分类器进行拟合；并且也无法使用有监督学习方法，往往只能使用无监督学习的方法来进行异常检测。

异常点的类型主要有以下三种：

全局离群点。即可以通过邻近性度量直接区分开；
情境离群点。在某种情境下，需要一定的先验知识，例如检测地区温度异常，需要考虑到地区的差异带来的温度差异，而不是仅仅考虑一个温度的数值差异；
集体离群点。同样需要先验知识，需要知道不同数据群体之间的邻近性度量的差异。

异常检测算法

孤立森林

孤立森林 (Isolation Forest) 是一个基于集成树模型的「无监督」异常检测算法。对于森林中的每一棵树，初始时含有所有的数据对象，每次对树的所有结点进行分裂，分裂规则为随机选择一个属性并随机选择一个分割点，然后基于这个分割点将结点中的数据对象划分为两部分，直到一个结点只含有一个数据对象或者达到最大深度时停止分裂。孤立森林中树之间的区别取决于分裂时选择的属性不同，这与决策树算法比较类似。

森林构造出来的，如何确定异常点呢？该算法定义第 \(i\) 个样本 \(x_i\) 的异常分数 \(s\) 为下式：

\[ s(x_i, N) = 2^{-\frac{E(h(x_i))}{c(N)}} \]

其中：

\(c(N)\) 表示数据集大小为 \(N\) 时每一个样本的平均路径长度；
\(E(h(x_i))\) 表示样本点 \(x_i\) 在所有树中的平均路径长度。

评判标准：

异常分数越接近 \(1\) 就表明当前样本点越有可能是异常点。因为此时样本点的平均路径很短，说明当前样本点很容易就被区分开了；
异常分数越接近 \(0\) 就越不可能是异常点。说明当前样本点在所有集成树上的平均路径很长，很难和别的样本区分开；
若数据集中样本点的异常分数都接近 \(0.5\) 就说明当前数据集没有异常点。说明数据集中的所有样本都很类似。

算法分析：

优点：计算效率更高；
缺点：不适用于高维稀疏的样本分布。难以发现集体离群点。

基于距离的异常检测

一句话概括就是如果一个数据对象的 \(r\) 邻域内数据对象个数不足阈值 \(k\)，则认为当前数据对象是一个异常点。代码实现时，双重 for loop 即可。

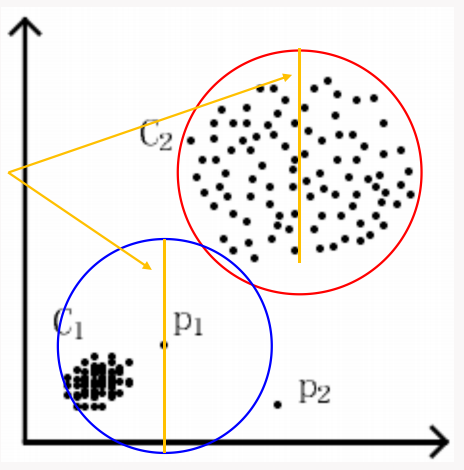
该法有一个很大的问题就是，超参数有两个，很容易出现不同超参导致聚类结果大幅波动的问题。比如下面的数据分布：

数据对象 \(P_1\) 邻域内的对象数量是满足阈值的，但是很容易看出来 \(P_1\) 是一个异常点。

基于密度的异常检测

基于密度的异常检测就可以规避上述基于距离的异常检测隐含的问题。这里介绍 LOF 算法，论文地址为：LOF: Identifying Density-Based Local Outliers

定义数据对象 \(x\) 的「k-距离 \(dist_k(x)\)」为全体数据对象中与其相距第 k 大的距离值。定义 \(N_k(x)\) 为全体数据对象中距离数据对象 \(x\) 的距离小于等于 k-距离的数据对象个数。于是可以得到以下两个指标：

数据对象 \(x\) 的局部可达密度 (local reachable density)：

\[ lrd_k = \frac{|N_k(x)|}{|N_k(x)| \times dist_k(x)} = \frac{1}{dist_k(x)} \]

Tip

我对上式做了简化。在原始的式子中，分母是当前数据对象 \(x\) 的邻域内所有数据对象 \(x'\) 的可达距离之和。可达距离定义为 \(\max{(dist_k(x), dist(x, x'))}\)，显然的邻域内数据对象 \(x'\) 到当前对象 \(x\) 的可达距离全都是 \(dist_k(x)\)，因此可以简化为上式。
数据对象 \(x\) 的局部离群点因子 (Local Outlier Factor)：

\[ LOF_k = \frac{\sum_{x'\in N_k(x)} \frac{lrd_k(x')}{lrd_k(x)} }{|N_k(x)|} \]

其中：

当 LOF 接近 1 时说明当前点和邻近点的密度相似，可能是正常点；
当 LOF 小于 1 时说明当前点的密度比邻近点更大，可能是簇中心；
当 LOF 远大于 1 时说明当前点的密度远小于邻近点的密度，可能是离群点。

说白了，就是给出了每一个数据对象的密度度量标准，然后看看邻域内点的密度和当前点的密度差异，就可以检测异常点了（至于为什么这么定义，鬼知道。反正在数据集上测出来的点数很高就行了，樂！）。