数据的表示和处理

计算机内部所有的信息都采用二进制 01 进行编码，而需要编码的数据分为数值数据和非数值数据两类。本章就从「数值数据的表示、非数值数据的表示、数据的存储、数据的运算」四个方面，介绍计算机的数据表示和处理方法。

数值数据的表示

数值数据主要有以下几种进制表示：

1. 二进制：后缀为 B（即 Binary，如 0110B）；
2. 八进制：后缀为 O（即 Octal，如 12673O）；
3. 十进制：后缀为 D（即 Decimal，如 291D，可省略）；
4. 十六进制：后缀为 H（即 Hexadecimal，如 3F9H；可以前缀 0x 标记，即 0x3F9）。

在进制转换时，一般先将数据转换为二进制，再进行相应转换。

整数的表示

机器中的整数全都是二进制，在实际表示时：

• 无符号整数：所有的二进制位都用来表示数值。比如对于 \(n\) 位的二进制数，无符号整数的数值范围为 \([0,2^{n} - 1]\)；
• 有符号整数：第一位二进制位必须用来进行正负性表示，后 \(n-1\) 位用来表示数值。同样对于 \(n\) 位的二进制数，有符号整数的数值范围为 \([-2^{n-1}, 2^{n-1})\)。

C 语言标准中规定：若运算中同时有无符号和带符号整数，则按无符号整数运算。搞懂下面这张真值比较表即可：

关系表达式	类型	结果	说明
0 == 0U	无	1	00…0B = 00…0B
-1 < 0	带	1	11…1B (-1) < 00…0B (0)
-1 < 0U	无	0	11…1B (2³²-1) > 00…0B (0)
2147483647 > -2147483647 - 1	带	1	011…1B (2³¹-1) > 100…0B (-2³¹)
2147483647U > -2147483647 - 1	无	0	011…1B (2³¹-1) < 100…0B (2³¹)
2147483647 > (int) 2147483648U	带	1	011…1B (2³¹-1) > 100…0B (-2³¹)
-1 > -2	带	1	11…1B (-1) > 11…10B (-2)
(unsigned) -1 > -2	无	1	11…1B (2³²-1) > 11…10B (2³²-2)

浮点数的表示

浮点数的基本结构。 浮点数是小数点位置可变的数，用以表示范围极大的实数。数学形式为：

\[ X = (-1)^{S} \times M \times R^E \]

其中：

• \(S\) 为符号位 (Sign) ，取 0 表示正，1 表示负；
• \(M\) 为尾数 (Mantissa) ，是一个定点小数，决定精度。有效位数越多，说明精度越高；
• \(E\) 为阶数 (Exponent) ，是一个定点整数，决定小数点位置；
• \(R\) 为基数 (Radix) ，由数制决定（在二进制系统中 \(R=2\)）。

这种表示方式使浮点数能在有限位宽下同时兼顾「范围」与「精度」。

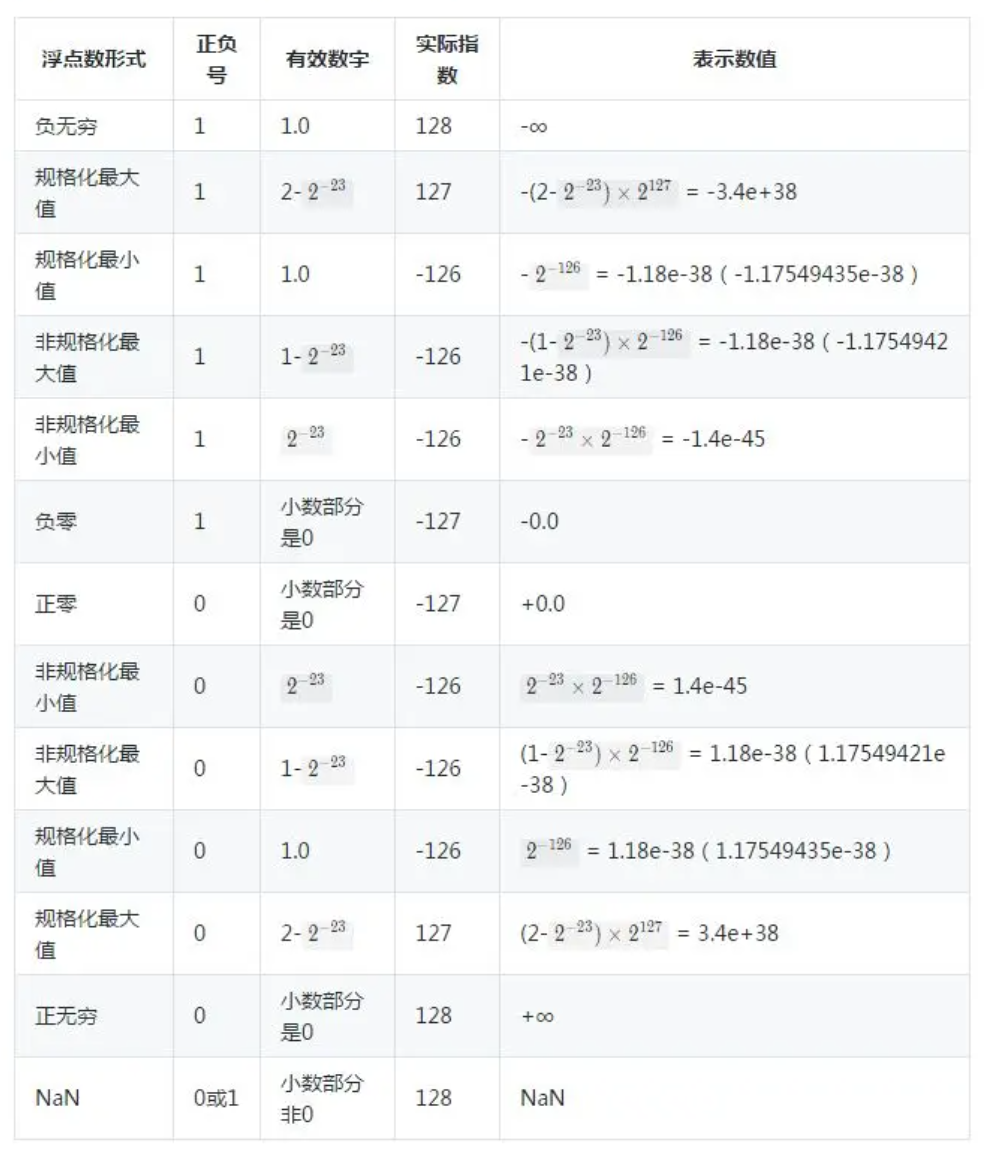
浮点数的取值范围。假定浮点数的尾数为纯小数即尾数不为零，则浮点数 \(X\) 的绝对值的最小值表示为 \(0.00...1 \times R^{-11...1}\)，最大值表示为 \(0.11...1 \times R^{11...1}\)。假设阶数为 \(m\)，尾数为 \(n\) 位纯小数，则浮点数 \(X\) 的绝对值真值的取值范围为：

\[ R^{-n} \times R^{-(R^m-1)} \le |X| \le (1-R^{-n}) \times R^{R^m-1} \]

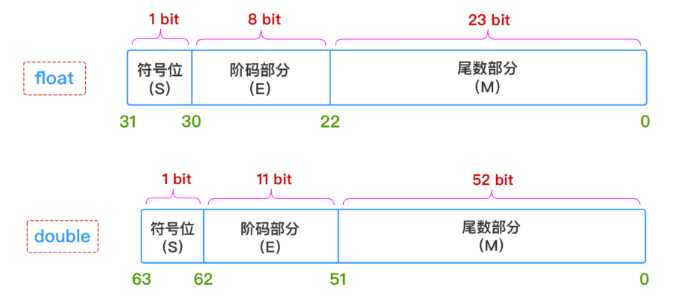
以 32 位二进制浮点数为例（单精度）：

• 第 0 位为符号位；
• 第 1–8 位为阶数位，采用移码形式，通常需要加上偏执常数（例如 128）；
• 第 9–31 位为尾数位，规格化形式为 \(0.1bb...b\)。

那么：

• 正数的最大值：\(0.11...1 \times 2^{11...1}=(1-2^{-24}) \times 2^{127}\)
• 正数的最小值：\(0.10...0 \times 2^{00...0} = 2^{-1} \times 2^{-128}=2^{-129}\)

具体如下图所示：

浮点数的规格化。 规格化 (Normalization) 指将尾数调整为唯一标准形式，使得最高有效位固定为非零。对于二进制浮点数，规格化尾数一般形如 \(1.xxxxxx\)。规格化的过程可分为：

• 左规：尾数过小，需左移并减少阶数；
• 右规：尾数过大，需右移并增加阶数。

规格化的意义在于：

1. 使浮点数表示唯一；
2. 保留尽可能多的有效位；
3. 保证计算结果在允许范围内保持最大精度。

IEEE 754 标准下的浮点数。现代计算机普遍采用 IEEE 754 标准来统一浮点数格式。

与前面提到的规则略有不同。对于下列两种精度的浮点数：

IEEE 754 有以下规定：

1. 对于阶数：同样采用移码的形式，即实际阶 = 存储值 − 偏移常数。只不过现在的偏执常数不是 \(2^{n-1}\)，而是 \(2^{n-1}-1\)。因此单精度浮点数（32 位）和双精度浮点数（64 位）的偏执常数分别为 \(2^{8-1}-1=127,2^{11-1}-1=1023\)；
2. 对于尾数：隐藏位 1 还是存在，不过现在不是在小数点右边，而是在小数点左边，即规格化数的实际尾数为 \(1.xxx...x\)。

IEEE 754 标准下，浮点数与真值的转换

IEEE 754 标准下，浮点数 5 种类型的表示方法

IEEE 754 标准下，单精度浮点数的各种极端情况

C 语言中的浮点类型。在 C 语言中，浮点类型的精度和范围与 IEEE 754 密切相关：

• int \(\to\) float：可能丢失有效数字，因为整数的有效位多于 float；
• int, float \(\to\) double：数值不变，精度提升；
• double, float \(\to\) int：可能发生溢出或舍入误差；
• double \(\to\) float：可能丢失有效数字或超出范围。

非数值数据的表示

计算机最基本的数据单位是位 (bit)，可以比较容易地表示数字。但现实世界中不仅有数字，还充满了文字、符号与逻辑判断。为了让计算机能处理这些“非数值”信息，人们设计了多种编码与表示方式。

逻辑值

计算机使用 1 位二进制数 表示一个逻辑值。例如 0 表示 False，1 表示 True。

西文字符

早期计算机主要用于处理英文文本，因此设计了美国信息交换标准代码 (American Standard Code for Information Interchange, ASCII)。

ASCII 用 7 位二进制编码，共可表示 128 个字符。其中：

• 0–31：控制字符（如换行、回车等）
• 32–126：可打印字符（如字母、数字、标点符号等）

有时，为了方便存储在一个完整的字节中，第 8 位被保留作 奇偶校验位 (Parity Bit)，用于检测传输错误。

ASCII 在英文世界中足够使用，但无法涵盖欧洲语言的变音符号，更无法表示中文。

汉字字符

汉字属于表意文字，数量庞大。仅常用字就超过七千个，远远超出 ASCII 的 128 个编码空间。为在计算机中表示汉字，人们设计了多字节编码系统，其中最典型的两种是 GBK 和 UTF-8。

GBK（GuoBiao Kuozhan，国家标准扩展）是对早期 GB2312 的扩展版本。GB2312 只收录了常用汉字约 6763 个，而随着社会和科学技术的发展，这个数量远远不够。于是 GBK 在 1995 年被提出，能表示约 2 万个汉字，包括繁体字、少数民族文字以及符号等。

GBK 的主要特点是：

• 兼容 GB2312：即原有编码不变，向后兼容；
• 双字节编码：每个汉字占用两个字节。例如，"中" 在 GBK 中的编码是 D6 D0，"国" 的编码是 B9 FA；
• 不兼容 ASCII 扩展：虽然保留了 ASCII 区，但在国际环境下容易产生乱码。

GBK 在 Windows 系统中使用广泛，是早期中文互联网的主力编码。但其局限也很明显：在不同国家和地区，各自制定了不兼容的编码标准（如日文的 Shift-JIS、韩文的 KS-C-5601），导致跨语言信息交换时常出现“乱码”问题。这就催生了更统一的方案——Unicode。

UTF-8 是 Unicode 的一种具体实现方式。它采用「变长编码」，即不同字符使用不同字节数表示，从而在节省空间与支持多语言之间取得平衡。

UTF-8 的规则如下（十六进制）：

• 英文字符使用 1 字节（与 ASCII 完全一致）。例如：'A' \(\to\) 41；
• 欧洲符号一般使用 2 字节。例如：'ε' \(\to\) CE B5；
• 汉字等东亚文字通常使用 3 字节。例如：'中' \(\to\) E4 B8 AD；
• 罕见符号或表情（emoji）使用 4 字节。例如：'😊' \(\to\) F0 9F 98 8A。

UTF-8 的最大优势是兼容性：早期英文文本不需要修改即可在 UTF-8 环境下正常显示。同时，它支持全球所有语言，因此成为互联网的默认编码。

数据的存储

计算机内部一切数据最终都以二进制形式存储与运算。

数据的表示宽度与单位

根据不同的层次，计算机有不同的数据表示宽度：

• 位 (bit)：二进制信息的最小单位，只能表示 0 或 1；
• 字节 (Byte)：最小的可寻址存储单位。1 Byte = 8 bit；几乎所有现代计算机的内存、文件大小等，都是以字节为基本计量单位；
• 字 (word)：计算机一次能处理的二进制数据长度，由体系结构决定。早期 16 位系统中，1 word = 16 bit。32 位系统中，1 word = 32 bit；64 位系统中，1 word = 64 bit。

在硬件层面，计算机的各个组成部分（CPU、总线、寄存器、存储器等）也都有相应的“宽度”指标，用来描述数据通路的能力。

• 数据通路宽度 (Data Path Width)：指数据在 CPU 内部传输通道（寄存器、总线、算术逻辑单元之间）中一次能并行传输的位数。数据通路宽度通常等于或接近字长，是衡量系统并行处理能力的重要参数；
• 总线宽度 (Bus Width)：CPU 与内存、外设之间数据线的数量。例如：32 位系统的系统总线宽度常为 32 位。64 位系统通常为 64 位。总线宽度影响一次数据传输的量，也影响内存带宽。

数据的存储和排列顺序

对于一个 32 bit 的数 1000 0000 0000 0000 0000 0000 0000 0110 而言，我们定义：

• 最高有效位 (Most Significant Bit, MSB)：上述 32 位数的最左边的一位 1；

• 最低有效位 (Least Significant Bit, LSB)：上述 32 位数的最右边的一位 0；

• 最高有效字节 (Most Significant Byte, MSB)：上述 32 位数的最左边的一字节 1000 0000；

• 最低有效字节 (Least Significant Byte, LSB)：上述 32 位数的最右边的一字节 0000 0110。

现代计算机都是按字节编址。由于程序中对每个数据只给定一个地址，那么对于多字节的数据如何根据仅有的一个地址进行内存分配呢？这就是经典的字节排序问题。现在介绍两种内存分配方式：

• 大端方式：最低有效字节存放在最高位。对应的机器码中最低有效字节在最右端；

• 小端方式：最低有效字节存放在最低位。对应的机器码中最低有效字节在最左端。

例如，对于机器数 0xFFFFFFF6 而言，下面的表示方式中，左侧为小端存储，右侧为大端存储：

数据的运算

高级语言中涉及到的各种运算，都会被编译成底层的运算指令，本目要介绍的就是其中的运算逻辑。

逻辑运算

主要有以下三种：

逻辑运算类型	C 语言中的符号	说明
逻辑或	||	有真则真
逻辑与	&&	都真为真
逻辑非	!	真假翻转

位运算

位运算类型	C 语言中的符号	说明
按位或	|	逐位逻辑或
按位与	&	逐位逻辑与
按位取反	~	逐位逻辑非
按位异或	^	逐位进行不进位加法
左移	<<	无符号整数采用逻辑移位，高位移出，低位补 0，如果移出为 1，则溢出；有符号整数采用算数移位，高位移出，低位补 0，如果左移前后符号位不同，则溢出
右移	>>	无符号整数采用逻辑移位，高位补 0，低位移出；有符号整数采用算数移位，高位补符号，低位移出
位扩展	内置逻辑	在短数向长数转换时。有符号整数采用符号扩展（前方补符号位）；无符号整数采用 0 扩展（前方补 0）
位截断	内置逻辑	在长数向短数转换时。高位直接丢弃

位扩展案例

#include <stdio.h>

int main() {
    short int si = -32768;
    unsigned short usi = si;
    int i = si;
    unsigned ui = usi;

    printf("si  = \t%hd\t%x\n", si, si);
    printf("usi = \t%hu\t%x\n", usi, usi);
    printf("i   = \t%d\t%x\n", i, i);
    printf("ui  = \t%u\t%x\n", ui, ui);
}

上述代码在 32 位大端机器上的输出：

si  =   -32768  8000
usi =   32768   8000
i   =   -32768  ffff8000
ui  =   32768   8000

分析：

• si 和 usi 是同一个机器数的不同真值结果，由于数位没有长短的变化，故十六进制表示结果相同
• i 是有符号整数的位扩展，采用符号扩展，补充符号位 1，故向前补充了 16 个 1
• ui 是无符号数的位扩展，采用 0 扩展，补充 0，故向前补充了 16 个 0

位截断案例

#include <stdio.h>

int main() {
    int i = 32768;
    short si = (short)i;
    int j = si;

    printf("i  = \t%d\t%x\n", i, i);
    printf("si = \t%hd\t%x\n", si, si);
    printf("j  = \t%d\t%x\n", j, j);
}

上述代码在 32 位大端机器上的输出：

i  =    32768   00008000
si =    -32768  8000
j  =    -32768  ffff8000

分析：

• i 的真值和机器数很显然
• si 的机器数就是将 i 的机器数截取了后 16 位的结果，在识别为有符号数以后，得到的真值就是最小的负数 -32768
• j 是有符号整数的位扩展运算，补充符号位 1
• 可以发现了 截断错误，而这种错误编译器一般是不会发现的！

整数加减运算

对于无符号整数和有符号整数而言，都可采用以下运算部件进行运算：

输入：

1. 运算数 A：整数 A 的补码 01 序列
2. 运算数 B：整数 B 的补码 01 序列
3. 判别数 Sub：A+B 时 Sub=0，A-B 时 Sub=1

输出：

1. 结果 Sum：表示整数 A+B 的计算结果

2. 零标志 ZF：表示 A+B 是否为 0

3. 符号标志 SF：表示计算结果 Sum 的有效范围内的最高位二进制数值

4. 溢出标志 OF：判断 有符号整数 的相加结果是否溢出。计算方式：

   • 若 A 与 B' 首位同号且与 Sum 的首位不相同，则计算溢出，OF = 1
   • 反之则计算未溢出，OF = 0

5. 进/借位标志 CF：判断 无符号整数 的相加结果是否溢出。计算方式：

   • 对于加法：此时的判别数 Sub = 0

     • 若有进位，即 Cout = 1，则对于当前加法器表示计算溢出，CF = 1
     • 若没有进位，即 Cout = 0，则没有计算溢出，CF = 0

   • 对于减法：此时的判别数 Sub = 1

     • 若有借位，则 Cout = 0，则对于当前加法器表示计算结果是负数，即计算溢出，CF = 1
     • 若没有借位，则 Cout = 1，则对于当前加法器表示计算结果是正数，即计算未溢出，CF = 0

   • 综上所述：\(\text{CF} = \text{Sub} \oplus \text{Cout}\)。

运算案例

对于两个机器数 x = 1000 0110 和 y = 1111 0110

加法：计算 x + y减法：计算 x - y对于 n = 8 的情况而言，数据范围是

\[ \begin{aligned} &\text{MUX}: \begin{cases} y' &= y \\ \text{Sub} &= 0 \end{cases} \\ &\text{Adder}: \begin{cases} x: & 1000\ 0110 \\ y'= y: & 1111\ 0110 \\ \text{Sub}: & 0 \end{cases} \\ &\text{Result}: 1 \ 0111\ 1100 \\ &\text{Signals}: \begin{cases} \text{ZF} = 0 \\ \text{SF} = 0 \\ \text{OF} = 1 \\ \text{CF} = 1 \end{cases} \\ &\text{Real Value}: \begin{cases} \text{signed}: &124(134+246-2^8)\\ \text{unsigned}: &124(134+246-2^8) \end{cases} \end{aligned} \]

\[ \begin{aligned} &\text{MUX}: \begin{cases} y' &= \overline{y} \\ \text{Sub} &= 1 \end{cases} \\ &\text{Adder}: \begin{cases} x: & 1000\ 0110 \\ y'=\overline{y}: & 0000\ 1001 \\ \text{Sub}: & 1 \end{cases} \\ &\text{Result}: 0 \ 1001\ 0000 \\ &\text{Signals}: \begin{cases} \text{ZF} = 0 \\ \text{SF} = 0 \\ \text{OF} = 0 \\ \text{CF} = 1 \end{cases} \\ &\text{Real Value}: \begin{cases} \text{signed}: &-112 \\ \text{unsigned}: &144(134-246+2^8) \end{cases} \end{aligned} \]

\[ \begin{cases} \text{signed}: &[-2^{n-1},2^{n-1}) &=& [-128,127] \\ \text{unsigned}: &[0,2^n) &=& [0,255] \end{cases} \]

整数乘除运算

整数乘法中。两个 n 位的整数相乘得到一个 2n 位整数，但是一般只保留低 n 位，高 n 位舍弃。

判断乘法溢出规则如下：

• 对于无符号整数乘法：若高 n 位全 0 则没溢出，反之溢出；
• 对于有符号整数乘法：若高 n 位全等于 低 n 位的首尾，则没溢出，反之溢出。

整数除法中。两个 n 位整数相除，「溢出异常和小数舍去」规则如下：

• 除了最小负数除以 -1 会发生溢出，以及除 0 会发生异常以外，其余情况全部是正常运算；
• 无论是带符号还是无符号，所有产生的小数部分全部舍弃，效果就是向 0 取整。

常量乘除运算

常量乘法运算中。由于直接当做整数进行乘法会导致更高的消耗，因此编译器一般会将其拆分为移位运算与加减运算的综合运算。比如表达式 x * 20 中的 20 会被二进制拼凑分解为 2^4 + 2^2，也就是将 x 左移 4 位的结果与 x 左移 2 位的结果相加。

常量除法运算中。同样由于时间开销极大，也是采用移位进行优化，但是与加法略有不同。

对于除数是一个 \(2^k\) 整数的形式时：

1. 若被除数是「无符号数」或者「有符号正数」，直接低位丢弃，高位按照相应的规则补齐；
2. 若被除数是「有符号负数」，且移出低位时有 1，则需要先将被除数加上 \(2^k-1\)，再执行第一步的操作。