存储

当机器有了记忆，就可以不用人为干预而自动运行，从而真正意义上实现了自动化的流程。本章主要学习计算机中的存储器件、存储策略以及数据交互逻辑。

现代计算机中有很多类型的存储器，核心功能都是存储数据，那为什么不统一成一种存储器呢？根本原因是 CPU 的计算速度远大于从存储器中访存数据的速度，因此我们不得不设计出可以匹配 CPU 计算速度的存储器结构。但这样的存储器造价极高并且存储量很小，因此我们只能退而求其次，从而诞生了现代计算机中的层次存储结构。从 CPU 开始依次为：寄存器 (Register)、缓存 (Cache)、内存 (Main Memory) 和 外存 (Secondary Memory)。这些存储器的访存速度逐渐降低。本章也将按照这样的顺序分别讲解相应的概念，然后从上帝视角并结合上面所有的存储层次，宏观地讲解 虚拟化 技术。最后补充介绍一下存储器中的 数据校验 策略。

缓存

缓存采用的随机存取存储器是 SRAM，即静态随机存取存储器。由于其速度快容量小且造价很高，因此适合做 cache 工作。SRAM 存储高低电平的方式是触发器。

为什么会有缓存

基于程序的局部性。从高级语言的逻辑进行理解不难发现，数据的重复访问往往集中在一个程序段中（例如循环），对应的指令和数据是连续存储的，因此程序在内存中运行时具有局部性。不断执行的某些指令和不断访问的某些数据就可以存入缓存中。这里根据局部性再衍生出「空间局部性」和「时间局部性」两个概念。

• 空间局部性简单来讲就是某些指令或数据「存储顺序和访问顺序的差异」。差异越小，空间局部性就越好；
• 时间局部性简单来讲就是某些指令或数据「短时间内重复访问的情况」。重复访问的越多，时间局部性就越好。

缓存的工作逻辑

前置知识。cache 一般被组装在 CPU 内部，便于和寄存器进行高效的数据交互。与此同时，设计者将 cache 和内存划分为由相同大小存储空间组成的存储器，这里 "相同大小的存储空间" 在 cache 中被称为行 (line) 或槽 (slot)，在内存中被称为块 (block)。为了知道 cache 中每一个行是否有效缓存了内存的信息，设计者对 cache 中的每一行设定了一个有效位来区分是否缓存了有效信息。

如上图展示的 CPU 读取内存信息的流程图。CPU 在得到内存中的某一个地址后需要访问该地址指向的信息。此时可以首先查询 cache，若果没有找到，再进行 cache 缺失处理并去内存中查询。

int a[M][N] {};

// 更快
for (int i = 0; i < M; i++)
    for (int j = 0; j < N; j++)
        A[i][j] = 1;

// 很慢
for (int j = 0; j < N; j++)
    for (int i = 0; i < M; i++)
        A[i][j] = 2;

知道了 cache 的工作原理后，上面两个代码段执行时间天壤之别的原因也就呼之欲出了。由于对数据进行访问时，不同的数据仅仅是地址的差异，而每一个数据的地址都是用加法器一步运算出来的，按道理并不会有任何时间开销的差异。那这几十倍的时间开销差异从何而来？其实就是缓存的功劳。通过将数据按块缓存，可以减少 CPU 访问内存的次数，而只需要从缓存中取数即可，从而大大降低了时间开销。

值得一提的是。如果数据/指令的大小比一个「缓存行」或「内存块」还要小，那缓存机制就没什么优势了。并且从上述讨论可以发现，缓存机制对于代码编写者和编译器而言都是 透明 的存在，是从物理层面上对程序进行的优化。

注意：在考虑 CPU 访存时间时，如果脱靶，不仅仅需要考虑访问内存的时间，还要考虑访问 cache 的时间。

缓存与内存的映射关系

1）直接映射（模映射）

映射关系。首先我们需要对内存块和缓存行进行编号。假设缓存一共有 \(k\) 行，那么第 \(i\) 个内存块就会唯一对应到第 \(i\ \%\ k\) 个缓存行。

访存机制。假设现在 CPU 需要访问一个地址 AR。如果没有缓存机制，那就直接到内存中访问这个地址对应的信息即可；在直接映射的缓存规则下应该如何访问呢？在块的大小是 2 的幂并且缓存行数 k 也是 2 的幂的情况下，可以将内存地址划分为：标记、cache 行号、块内地址三个部分。前两个部分其实直接对应了内存中的哪一块，只不过在模映射规则下，可以先通过「cache 行号」的比较结果来判断是否需要继续进行标记匹配。具体的，如果此时 cache 行号匹配成功 && 标记匹配成功 && cache 的这一行是有效行，那就算命中了，此时地址译码器就直接返回 cache 中当前地址 AR 存储的数据/指令；反之如果 cache 行号匹配失败 || 标记匹配失败 || cache 的这一行不是有效行，那就算脱靶，此时就需要到内存找这个地址对应的数据/地址并返回，同时需要把这个地址在所在的块复制一份到 cache 对应的行。

工作特点。这种缓存方式的优点在于可以在一定程度上减少地址的匹配位数。但是越简单的东西 缺点 也一定越明显，这种策略很可能造成极端情况发生，即某些被频繁访问的内存块对应的 cache 行号是一样的，这就无法利用上别的闲置的行，并且会导致 cache 对应的行被一直被替换，起不到缓存的作用。

2）全相联映射

映射关系。内存中的每一个块可以缓存到任意一个 cache 行中。

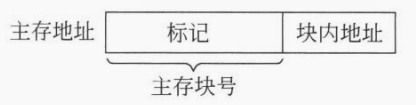
访存机制。内存地址从高位到低位被划分为：标记和块内地址。地址译码器根据 CPU 发出来的地址进行解析之后，遍历 cache 中所有的行进行标记匹配。

特点。显然的全相联映射的 优点 在于直接解决了模映射策略中不断遇到模数相等需要不断替换的极端情况。缺点 在于丢失了模映射的匹配优势，每一次匹配都需要完全匹配所有的标记。

3）组相联映射

映射关系。对于 N 路组相联，cache 中每一个组含有 N 个 cache 行，组间进行直接映射，组内全相联映射。

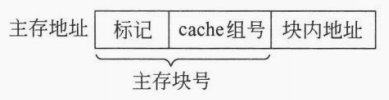
访存机制。内存地址从高位到低位被划分为：标记、cache 组号和块内地址。首先用内存块号 \(\%\) cache 的组数得到当前内存块在 cache 中的组号，然后遍历当前组中所有的 cache 行进行标记匹配和标志位判断。

特点。综合了直接映射和全相联映射的 优点，既可以避免频繁替换的极端情况，也可以加快地址的匹配速度。

缓存的替换算法

不难发现，在上述三种映射策略中，除了模映射是一一对应可以直接替换以外，另外两种映射策略需要考虑替换哪一个缓存行。有如下几种缓存的替换算法。

1）最佳时间 (Optimism Time, OPT)

算法思想就是提前预知所有内存块的调度顺序，然后每次需要替换时替换后续最后才需要访问的缓存行。这种方法显然不切实际，但是可以作为基准来度量其他替换算法算法的性能。

2）先进先出 (First In First Out, FIFO)

算法比较简单，就是一个队列算法。当然实际技巧是，每次标记队头缓存行，一旦脱靶就替换队头对应的缓存行，然后将下一行标记为队头即可。这种算法会产生「Belade」异常，所谓的 Belade 异常就是缓存行数量与命中次数不成正比，其他的替换算法都不会出现这种情况。

3）最近最少使用 (Least Recently Used, LRU)

算法也比较简单。实现技巧在于给每一个 cache 行一个计数器，从而找到最近最久未被使用的 cache 行进行替换。

Warning

这里的计数器就是给每一个 cache 行增加合适的标记位。至于位数的多少，取决于 LRU 的执行范围。例如采用 N 路组相联映射时的 LRU 算法，如果每一组有 16 个 cache 行，那么这里关于 LRU 替换算法就需要 4 个标记位。

4）最不经常使用 (Least Frequently Used, LFU)

5）时钟页面调度 (Clock)

采用循环指针，每一个调度内存的页面只有 0 和 1 两种状态。当首次被调入或者再次访问内存中某个实页（页框）时，将其标志位定义为 1，并让指针后移一位。当且仅当某个实页为 0 并且指针指向当前实页时，就将其调出。

综合例题

问：假定计算机系统有一个容量为 \(32K\times 16\) 位的主存，主存按字编址，每字 \(16\) 位。且有一个数据区容量为 \(4K\) 字的 \(4\) 路组相联 cache，采用 LRU 替换算法。主存和 cache 之间数据交换块的大小为 \(64\) 字。假定 cache 开始为空，处理器顺序地从存储单元 \(0,1,\cdots,4351\) 中取数，一共重复 \(10\) 次。设 cache 比主存快 \(10\) 倍。试分析 cache 的结构和主存地址的划分，并说明采用 cache 后速度提高了多少？

答：

• cache 的结构。由于 cache 的数据区容量为 4K 字，根据传输的数据块大小 64 字可以很容易算出 cache 一共有 4K/64 = 64 行。由于是 4 路组相联，因此 cache 一共有 16 组，每组 4 行。

• 主存地址的划分。根据主存总容量 32K 字，以及传输的数据块大小 64 字可以很容易算出主存一共有 32K/64 = 512 块。每一个块对应到 cache 16 个组中的一个，因此主存结构如下：

  标记	cache 组号	块内地址
  5 位	4 位	6 位

• 速度提升。由于取数是对应 \([0,4151]\) 共 \(4152/64=68\) 块，因此本质上只访问了内存中的 \(68\) 块数据。初始的 \(64\) 块数据需要全部访问内存获取，最后 \(4\) 块由于需要替换也需要从内存获取。因此第一轮需要访问内存 \(68\) 次。不难发现，在 LRU 算法下，后续的 \(9\) 轮都是在对前四组中的 cache 行替换 \(5\) 次，因此后续的 \(9\) 轮每一轮都需要从内存访问 \(20\) 次。那么命中率 \(P\) 为：

  \[ P =\frac{43520-68-20\times 9}{43520}\approx99.43\% \]

  速度提升的倍数为：

  \[ \frac{T_m}{P\times T_c + (1-P)\times(T_m+T_c)} = \frac{10}{99.43\% \times 1 + (1-99.43\%)\times (10 + 1)}\approx 9.46 \]

缓存与内存的一致性

CPU 在执行写操作时，可能会写入 cache，为了保证 cache 和内存的一致性，提出了以下两种策略：

1. white through。如果写命中 cache，就同时写 cache 和内存；如果写不命中 cache，要么只写内存，要么写完内存后将更新过的内存块添加到 cache 中；

2. white back。如果写命中，就只写 cache；如果写不命中，就从内存中调入对应的内存块然后在 cache 中进行写入。

   Warning

   这种方法需要给每一个 cache 行增加一个标记位来表示是否需要进行写回操作。

可以发现上述 white through 策略可以绝对确保 cache 和内存的一致性，但是由于写如内存操作的开销很大，因此这种方法带来的性能损失也很大。相反 white back 策略就只会写入 cache，对应的开销就小很多，但是显然会出现 cache 和内存的不一致问题，这种策略需要结合别的策略来确保 cache 和内存的一致性。

内存

内存采用的随机存取存储器是 DRAM，即动态随机存取存储器。相比于 SRAM，DRAM 速度较慢但容量更大，因此适合做内存工作。DRAM 存储高低电平的方式是电平，即通过电容的高低电平状态来存储 01 状态。由于 DRAM 的读操作会对高电平进行放电，因此需要定时对 DRAM 的电容进行充电，也就是所谓的按行刷新。

部分内容参考：深入内存/主存：解剖 DRAM 存储器

内存的工作逻辑

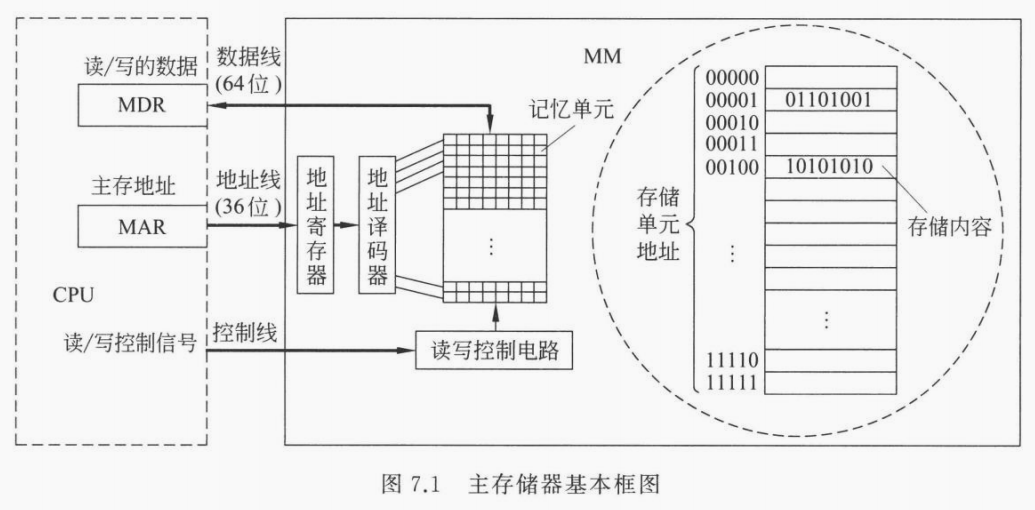
上图与缓存的工作逻辑类似，隐藏了 cache，突出了地址译码的逻辑。

CPU 首先通过「控制线」将读/写信号送到内存，然后分读写两种情况：

1. CPU 需要读数据时。就将需要读取数据的地址通过「地址线」送到内存寻找相应的数据，内存通过「数据线」将数据返回给 CPU；
2. CPU 需要写数据时。就将需要写入数据的地址通过「地址线」送到内存寻找待写入的内存，同时将需要写入的数据通过「数据线」送到内存并写入指定的内存中。

CPU 与内存的数据通信分为异步和同步两种：

1. 异步。CPU 从数据线取数时需要收到内存已经准备好数据的信号；
2. 同步。CPU 从数据线取数无须内存的信号，而是在向内存发出取数信号后，经过确定的时间后就从数据线取数。

地址译码器

如果有 \(n\) 位地址位，就决定了寻址范围为 \([0,2^n-1]\)。不难发现如果是一维单译码，就需要译码器有 \(2^n\) 个译码寻址线。如果是二维双译码，就只需要译码器有大约 \(2 \times 2^{n/2}\) 个译码寻址线。显然当地址位较多时，二维双译码器是更优的。

芯片扩展

芯片扩展分为「字扩展、位扩展和字位同时扩展」三种。已经在数电中学习过了，不再赘述。

外存

外存在计算机组成原理课程中几乎没有讲到（悲），在 OS 课程中简单讲解了磁盘存储系统，也没什么意思。这里就待完善吧。