静态词嵌入
本章介绍静态词向量学习任务。
基本概念¶
词 / token¶
NLP 中的「词」一般指对应语言的最小表示单位,约定上称为「token」。
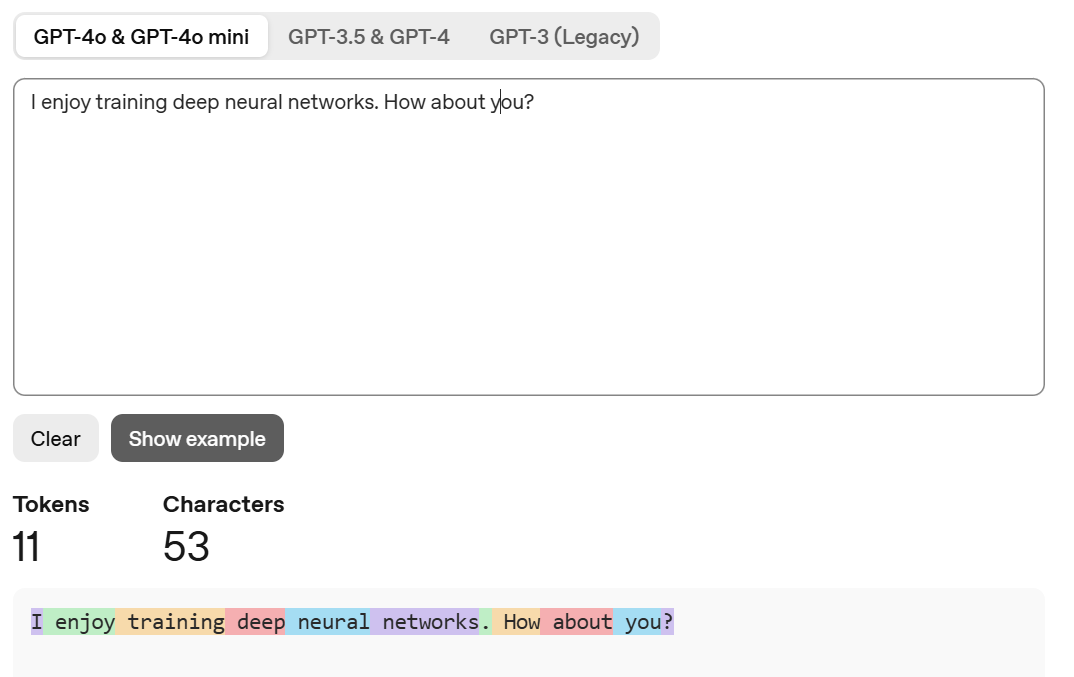
使用 OpenAI Tokenizer 表示的句子中的 token 分布如下:
词的表示方法¶
传统 NLP 任务中,词都是以独热编码 (One Hot) 的方式表示,即每一个词都表示为一个「只含有一个非零元素」的向量,向量大小为词典大小。由于独热编码向量之间都是正交的,这就导致没法计算单词之间的相似性,也就难以从语义上进行 NLP 任务,所以传统 NLP 中词的表示方法都是基于统计的(例如 Bag of Words、TF-IDF 等)。
如何用向量表示语义呢?词表示学习应运而生。
研究者们通过设计任务,让模型学习出每一个单词的表示向量,这样的模型就叫做「词向量模型」,学到的表示向量叫做「分布式向量」。
Tip
上述方法得到的词向量是静态的,因为仅仅基于固定的语料,下游任务语料的词分布往往是复杂多变的,所以最佳方式其实是每个任务额外训练词向量(即动态词向量),但这往往需要更多的成本。考虑到此处为入门示范,仅讨论如何训练这样的词向量,感兴趣的读者可以移步 大模型专栏 作进一步阅读。
性能度量¶
为了评估学习出来的词向量,最粗暴的方法就是看看这些词向量在下游任务上的影响程度,但这样比较费时间。其他的评估方法主要有两种:word analogy、word similarity。
word analogy,即单词类比。测试集构造了多个 a - b = c - d 的文本对,测试词向量时,给定 \(a\)、\(b\) 和 \(c\),根据余弦相似度找到使得 \(c - d'\) 最接近 \(a - b\) 的 \(d'\) 向量,看看 \(d'\) 对应的文本是不是 \(d\) 对应的文本,得到一个二分类的 accuracy 评估指标。
word similarity,即单词相似性。测试集构造了多个 a: word, b: word, similarity: float 的数据对(人工标注的),然后使用预算相似度计算词向量之间的 similarity 降序排序,计算金标排序和预测排序之间的斯皮尔曼秩相关系数 (Spearman Rank Correlation) 得到评估指标。其中斯皮尔曼秩相关系数的计算公式如下:
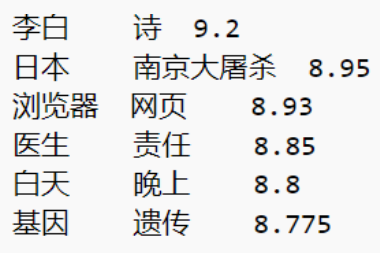
例如有一组测试金标如下:
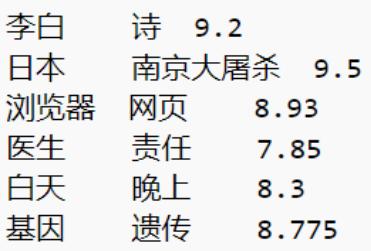
学习出来的词向量之间的余弦相似性计算如下:
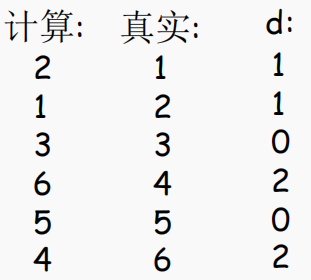
就可以计算金标排序和预测排序之间的差异:
于是最终的斯皮尔曼秩相关系数就是:
Word2Vec¶
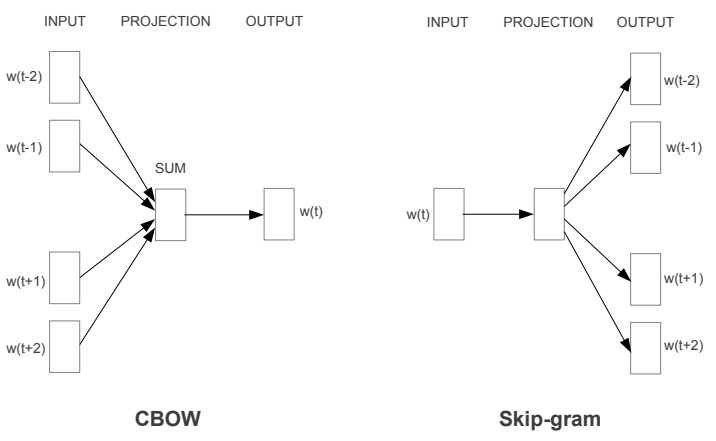
论文 1 提到了两种学习架构,如下图所示:
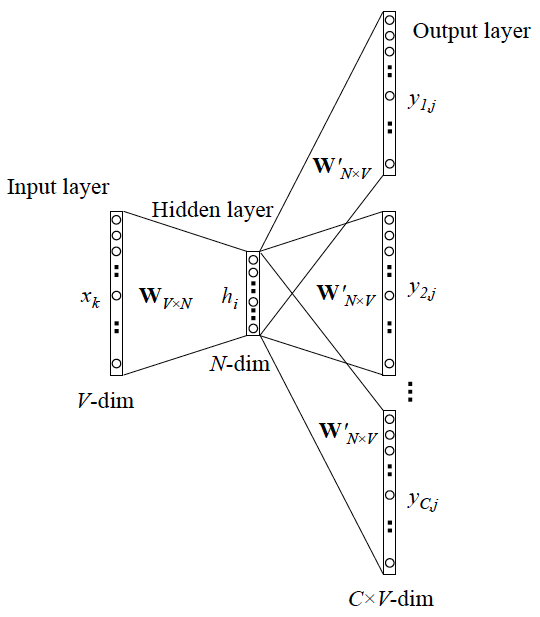
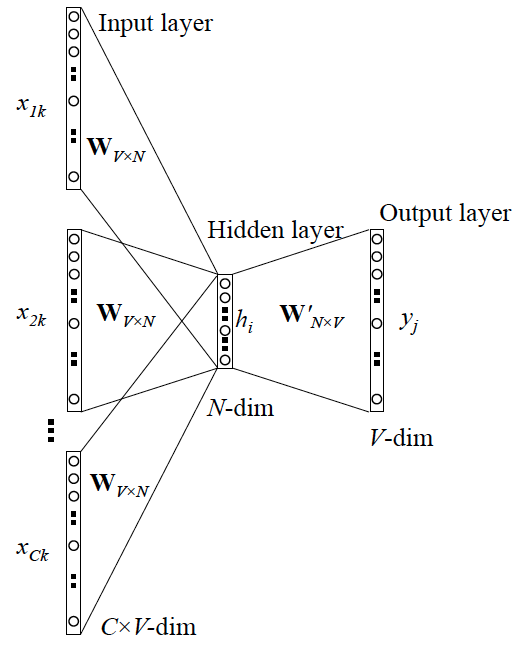
记词典大小为 \(V\),隐藏层大小为 \(N\)。其中:
- 从 INPUT 到 PROJECTION 使用一个线性映射,对应权重矩阵 \(W_{V\times N}\);
- 从 PROJECTION 到 OUTPUT 使用另一个线性映射,对应权重矩阵 \(W_{H,N}\)。
窗口大小论文中用的 \(10\),即分别取当前单词的前五个和后五个作为上下文,每个单词(图中箭头)线性映射结束后求和取平均得到当前窗口的 hidden state,于是 Word2Vec 的模型就介绍完了。下面讲讲损失函数是怎么设计的。
Skip-gram¶
连续跳跃语法 (Continuous Skip-gram) 模型是论文提到的一种分布式向量学习方式。其核心思想是在一个定长窗口内,最大化下式:
训练语料中所有单词数量为 \(T\),当前单词为 \(w_t\),模型总参数为 \(\theta\)。现在对上式进行等价变换,得到平均负对数似然函数:
使用 softmax 函数归一化所有的概率然后进行随机梯度下降即可优化得到最终的 \(\theta\)。当然这里的 \(\theta\) 其实就是 \(W_{V\times N},W'_{N,V}\) 两个权重矩阵。
CBOW¶
连续词袋 (Continuous Bag-of-Words, CBOW) 模型是论文提到的一种分布式向量学习方式。与 Skip-gram 同理,就不赘述了。
GloVe¶
区别于 Skip-gram 和 CBOW,GloVe 2 模型的训练并没有使用神经网络,而是利用共现矩阵的信息训练出分布式向量的。
记词典大小为 \(V\),共现矩阵(一般是对称的)为 \(X_{V\times V}\),作为中心词的词向量为 \(w\),对应的偏置为 \(b\),作为上下文词的词向量为 \(\tilde w\),对应的偏置为 \(\tilde b\),其中 \(w\) 和 \(\tilde w\) 分别使用随机初始化。则 GloVe 的损失函数为:
我们可以将其看作一个增强鲁棒的均方误差损失,优化后每个单词都会学出一个 \(w\) 和 \(\tilde w\),将其逐位相加就得到了最终的分布式词向量。
几个值得思考的地方,我们从左往右进行:
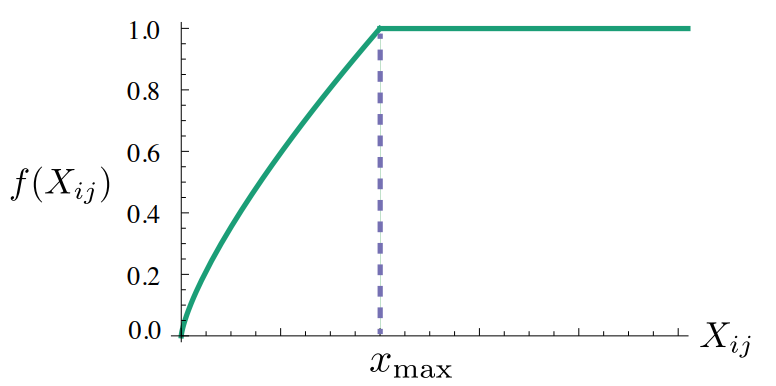
1)为什么要定义 \(f(\cdot)\) 函数
这是是作者自定义的映射函数:
其中 \(x_{\max}=100,\alpha=0.75\),目的是为了跳过 \(X_{ij}=0\) 的词向量对,这种词向量对对于最终的学习是没有贡献的;同时需要降低对高频词对的关注,提升对低频词对的关注。\(f(\cdot)\) 对应的图像如下:
2)\(w_i^T \tilde w_j\) 有什么意义
作者认为,向量内积可以用来表示两个向量之间的距离。
3)为什么要加 \(b_i,\tilde b_j\) 这两个偏置
偏置项的存在使得模型不必强行通过调整向量方向来拟合所有共现频率,从而减少语义信息的失真。
4)为什么要给共现频率加上 \(\log\) 函数
同样是为了降低对高频词对的关注度,提升对低频词对的关注度。
-
Mikolov T , Chen K , Corrado G ,et al.Efficient Estimation of Word Representations in Vector Space[J].Computer Science, 2013.DOI:10.48550/arXiv.1301.3781. ↩
-
Jeffrey Pennington, Richard Socher, and Christopher Manning. 2014. GloVe: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 1532–1543, Doha, Qatar. Association for Computational Linguistics. ↩