网络增强

我们希望神经网络的拟合结果既满足低偏差，又满足低方差，就需要从网络结构、训练策略等角度进行调整。一般来说，低偏差表示对网络进行优化，低方差表示对网络进行正则化。这里将其统一称作「网络增强」。

修改网络结构

逐层归一化、ReLU 激活函数、残差连接。

修改优化算法

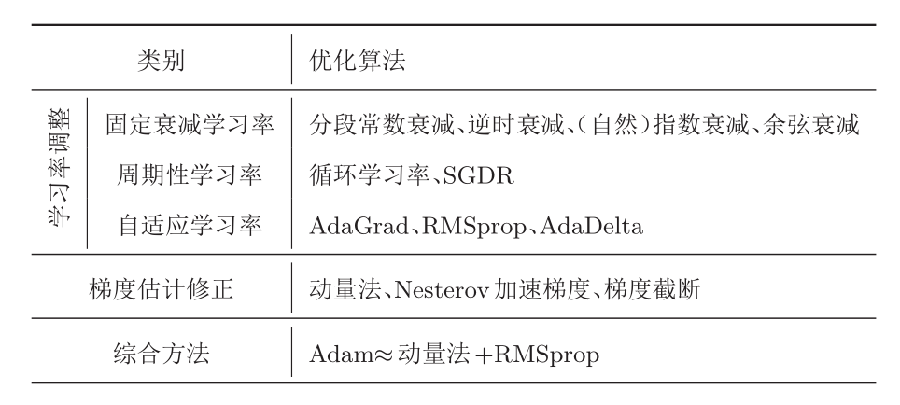
对于可训练的参数：

对于不可训练的参数：

• 层数
• 每层神经元个数
• 激活函数
• 学习率（以及动态调整算法）
• 正则化系数
• mini-batch 大小

超参数优化方法：

• 网格搜索
• 随机搜索
• 贝叶斯优化
• 动态资源分配
• 神经架构搜索

mini-batch 与学习率的关系。对于网络中的超参数，如何进行选择呢？最朴素的方法就是网格搜索。对于随机梯度下降的参数优化算法，批大小与学习率一般成正比，即一批训练数据量越多，学习率越高。这是因为一批的训练数据越多，泛化能力就越高，对应的学习率就没必要太低。

学习率的动态调整算法。一般来说就是两个阶段，在初期的阶段，学习率线性增长，在之后的阶段中，学习率逐渐衰减。详情见 Facebook 的这篇论文 Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour [2018]。

下图展示了预热学习率调整的学习效果。图源：Bag of Tricks for Image Classification with Convolutional Neural Networks [2018]。

修改参数初始化方法

基于「范数保持性」的参数初始化方法。