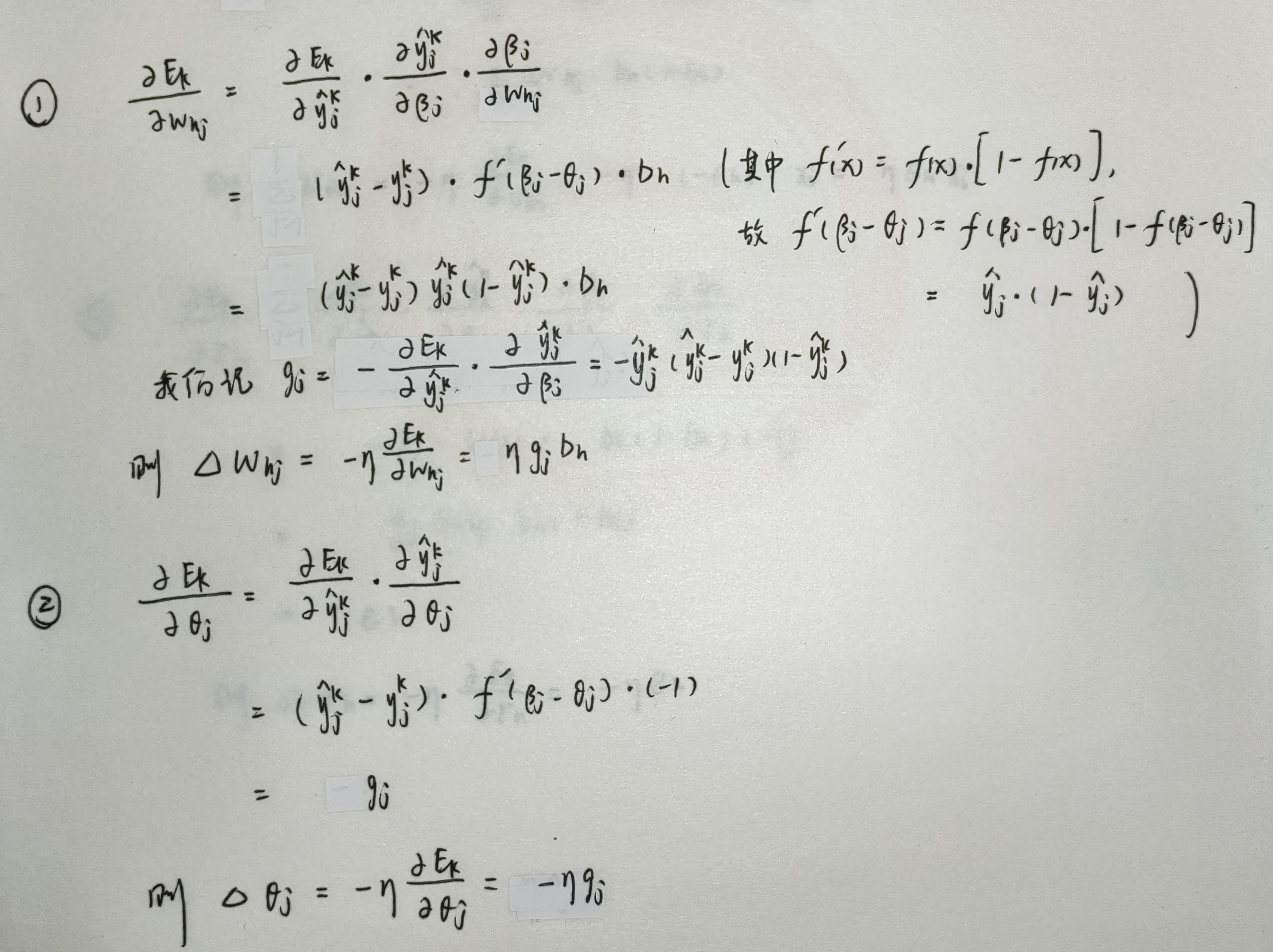全连接神经网络
全连接神经网络 (Full-connect Neural Network, FNN)，又称多层感知机 (Multi-Layer Perceptron, MLP)。是前馈神经网络 (Feedforward Neural Network, FNN) 的一种。是深度神经网络模型的开山鼻祖，通过向前传递数据，向后更新参数，实现学习和拟合的功能。
人工神经元
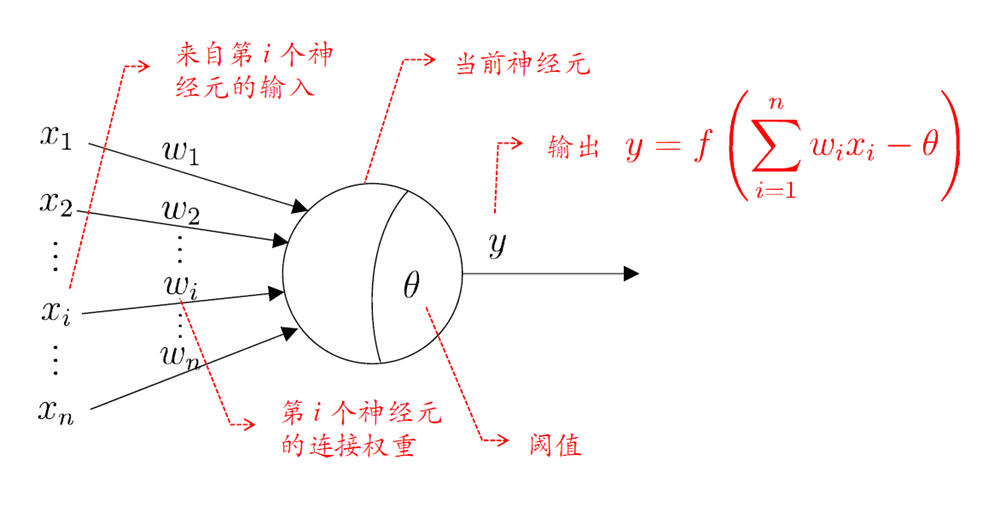
神经元是网络模型中的最小学习单元。每一个神经元接受输入 \(\sum_{i=1}^n w_ix_i - \theta\)，通过设定好的激活函数 \(f\) 得到该神经元对应的输出值 \(f(\sum_{i=1}^n w_ix_i - \theta)\)。其中 \(\theta\) 可以理解为神经元的激活阈值，也可以理解为神经元模型中的偏置项。
神经元中的激活函数大有门道、种类极多。为了确保网络可以拟合复杂的映射关系，需要激活函数是「非线性」的；为了便于对网络求导从而进行参数更新，需要确保激活函数是「可导」的；为了防止对网络求导的过程中出现梯度消失或者梯度爆炸，需要确保激活函数是「单调并且有界」。主要有以下 3 种类型：
- S 型函数。例如 Sigmoid 函数、Tanh 函数；
- 斜坡函数。例如 ReLU 函数；
- Swish 函数。复合函数。
FNN 模型
Tip
在神经网络模型中，我们定义输入层为前，输出层为后。
功能简介。所谓全连接神经网络，就是各层神经元之间不会跨层连接，也不存在同层连接，其中：
- 输入层仅仅接受外界输入，没有函数处理功能；
- 隐藏层和输出层进行函数处理。
神经元的输入与输出。分为「有函数处理功能」和「无函数处理功能」两类：
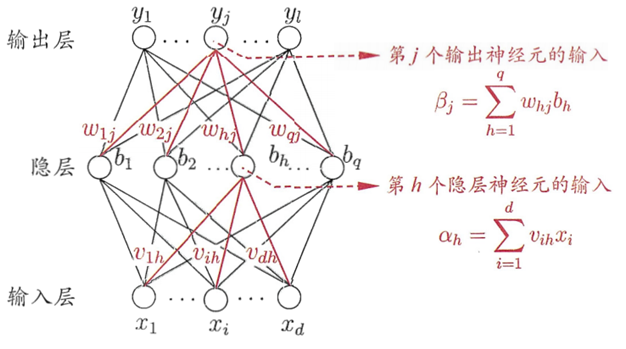
- 隐藏层：对于隐藏层的第 \(h\) 个神经元
- 输入：\(\alpha_h = \sum_{i=1}^dx_i v_{ih}\)
- 输出：\(b_h = f(\alpha_h - \gamma_h)\)
- 输出层：对于输出层的第 \(j\) 个神经元
- 输入：\(\beta_j=\sum_{h=1}^q b_h w_{hj}\)
- 输出：\(\hat y_j = f(\beta j - \theta_j)\)
网络参数。现在给定一个训练集学习一个分类器。其中每一个样本都含有 \(d\) 个特征，\(l\) 个输出。每输入一个样本都迭代一次。对于单隐层神经网络而言，一共有 4 种参数，即：
- 输入层到隐层的 \(d \times q\) 个权值 \(v_{ih}(i=1,2,\cdots,d,\ h=1,2,\cdots,q)\)
- 隐层的 \(q\) 个神经元的阈值 \(\gamma_h(h=1,2,\cdots,q)\)
- 隐层到输出层的 \(q\times l\) 个权值 \(w_{hj}(h=1,2,\cdots,q,\ j=1,2,\cdots,l)\)
- 输出层的 \(l\) 个神经元的阈值 \(\theta_j(j=1,2,\cdots,l)\)
FNN 学习准则
假设每次输入一个训练样本进行参数更新（即 batch size = 1）。由于网络输出内容是实数，因此我们定义目标函数 \(\mathcal L\) 为当前训练样本的「均方误差」。那么对于第 \(k\) 个训练样本，就有如下损失：
其中：为了求导方便，添加一个常量 \(\dfrac{1}{2}\)。\(\hat y\) 为样本真实值，\(y\) 为样本预测值。
FNN 优化算法
在进行梯度下降时，经过简单的推导可以发现，第 \(l\) 层的损失 \(\delta (l)\) 依赖于后一项的损失 \(\delta(l+1)\)，于是参数更新的逻辑就是从输出层开始逐层往后更新，直到第一层隐藏层。为此，我们引入著名的优化算法：误差逆传播算法 (error Back Propagation, BP)，其算法流程如下图所示：
以上述单隐层神经网络为例，尝试推导参数更新的过程。假定学习率（搜索步长）为 \(\eta\)，那么上述 4 种参数的迭代公式就为：
其中，修正量分别为：
利用链式法则推导修正量
