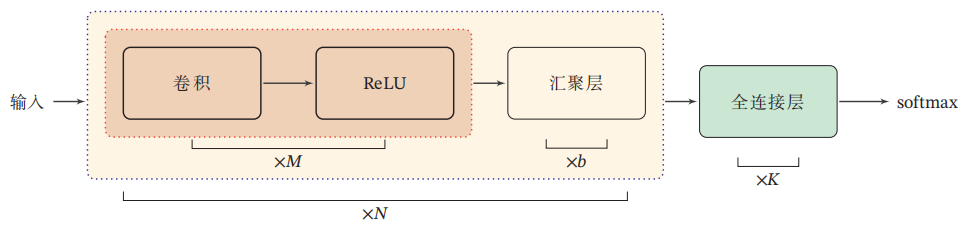
卷积神经网络
卷积神经网络
为了解决全连接网络「不能学习到局部不变性」以及「参数量过大」的缺点，卷积神经网络 (Convolutional Neural Network, CNN) 应运而生。卷积网络有三大特征：局部连接、权重共享、时/空上的次采样（汇聚/池化）。
卷积基本概念
统一表述。卷积是加权平均运算，属于线性运算。如果不对卷积核翻转，那么其实是叫「互相关」运算，真实的卷积是需要对卷积核翻转 180 度后再进行加权平均运算。为了统一：
- 语言描述上：由于卷积网络中的卷积核是可学习的并且与是否翻转无关，为了统一表述，后文提到的卷积运算都指互相关运算，即不翻转的加权平均操作；
- 符号表示上：理论上互相关运算记作 \(\otimes\)，卷积运算记作 \(*\)，后文统一用 \(\otimes\) 表示卷积运算。
基本术语。下面简单介绍一些在卷积神经网络中的术语：
- 滤波器 (Filter) 与卷积核 (Convolutional Kernel, K) 概念一致，指的是同一个东西；
- 特征映射 (Feature Map)：卷积运算后的结果，可以理解为卷积操作后提取出的特征；
- 感受野 (Receptive Field)：神经元对原始输入的感受范围，越深的神经元感受野就越大；
- 通道 (Channel, C)：在二维卷积中，通道数就是图像的深度，在一维卷积中（例如 NLP 任务），通道数就是词向量的维度；
- 移动步长 (Stride, S)：卷积核在输入数据中每次移动的长度；
- 零填充 (Zero Padding, P) 操作通过给输入数据的边缘填充 \(0\)，从而可以让输入数据的每一个位置之间被等价处理；
- 卷积核大小记作 (Kernel Size, K)。
卷积方式。
- 等宽卷积：通过零填充让输入与输出的大小相同；
- 宽卷积：通过零填充让每个输入点参与卷积运算的次数相同；
- 窄卷积：不做任何零填充操作。
CNN 模型
卷积层。对于二维卷积而言，我们假设输入共有 D 个图像，需要学习 P 个特征，并不是只需要学习 P 个卷积核的，对于每一个特征需要单独对每一张图像学习一个卷积核，因此需要学习 \(D\times P\) 个卷积核。
汇聚/池化层。从上面的卷积层学习逻辑可以看出其实参数量和全连接层相比还是很大。池化层就是通过减小输出数据的尺寸来大幅降低参数量；通过池化也可以起到去噪作用；可以看作一种特殊的卷积操作。常见的池化操作有：最大池化、平均池化。
全连接层。以分类任务为例，将上述汇聚后的结果展平 (flatten) 为一个向量，再进行 softmax 即可。
现代卷积网络详见 计算机视觉，这里不再展开。
CNN 学习准则
同样是反向传播算法通过梯度下降进行优化。
CNN 优化算法
TODO