跳转至

图像超分

本文简单介绍一种底层图像任务：图像超分辨率 1。

基本概念

任务定义

图像超分辨率 (Image super-resolution, SR) 顾名思义就是将低分辨率 (low resolution, LR) 图像转化到高分辨率 (high resolution, HR) 图像的过程。可以简单地理解为全局放大。

传统超分方法在 数字图像处理 中有过介绍，根据算法的不同分为「最近邻插值、双线性插值和双三次插值」共三种。但随着深度学习技术的成熟，基于深度学习的超分性能已经显著优于传统方法。本文将全方位展开基于深度学习方法的图像超分策略。

数据集

首先需要明确的一点就是，超分肯定是有监督策略，即同时需要一张图像的「低分和高分」图像对，自然条件下肯定是很难获得的，但是我们可以很容易地构造出这样的图像对。具体地，这里以退化核已知的构造方法为例，将原始图像看作高分图像，然后通过双三次插值对原始图像进行下采样即可得到低分图像。

因此超分的数据集很容易获得，只要来点高分辨率图像就行了，常见用来做超分任务的数据集有：Set5、Set14、Urban100、BSD100、Manga109 等，名称最后的数字就表示该数据集的图像数量。这些数据都可以在 huggingface 上找到。

性能评估

在得到超分辨率图像 (SR) 后，我们需要对其进行量化评价，人工评价的方法固然可行，但是在大规模数据集上肯定不可取，这就需要一些自动评价方法。我们记超分图像为 S，高分图像为 H，宽为 w，高为 h，则针对单通道的评价指标有以下三种：

均方误差 (Mean Square Error, MSE)。如下公式：

\[ \mathrm{MSE}(S,H) = \frac{1}{w h} \sum_{i=0}^{w-1}\sum_{j=0}^{h-1}(H_{ij}-S_{ij})^2 \]

显然 MSE 越小越好。

峰值信噪比 (Peak Signal-to-Noise Ratio, PSNR)。如下公式：

\[ \mathrm{PSNR}(S,H) = 10\cdot \log_{10}\frac{\max^2(H)}{\mathrm{MSE}(S,H)} \]

其中 \(\max(H)\) 表示原图的最大像素值。PSNR 单位为 dB，越大越好。

结构相似性 (Structural SIMilarity, SSIM)。

SRCNN

SRCNN 2 是利用深度学习方法进行图像超分的开山之作。

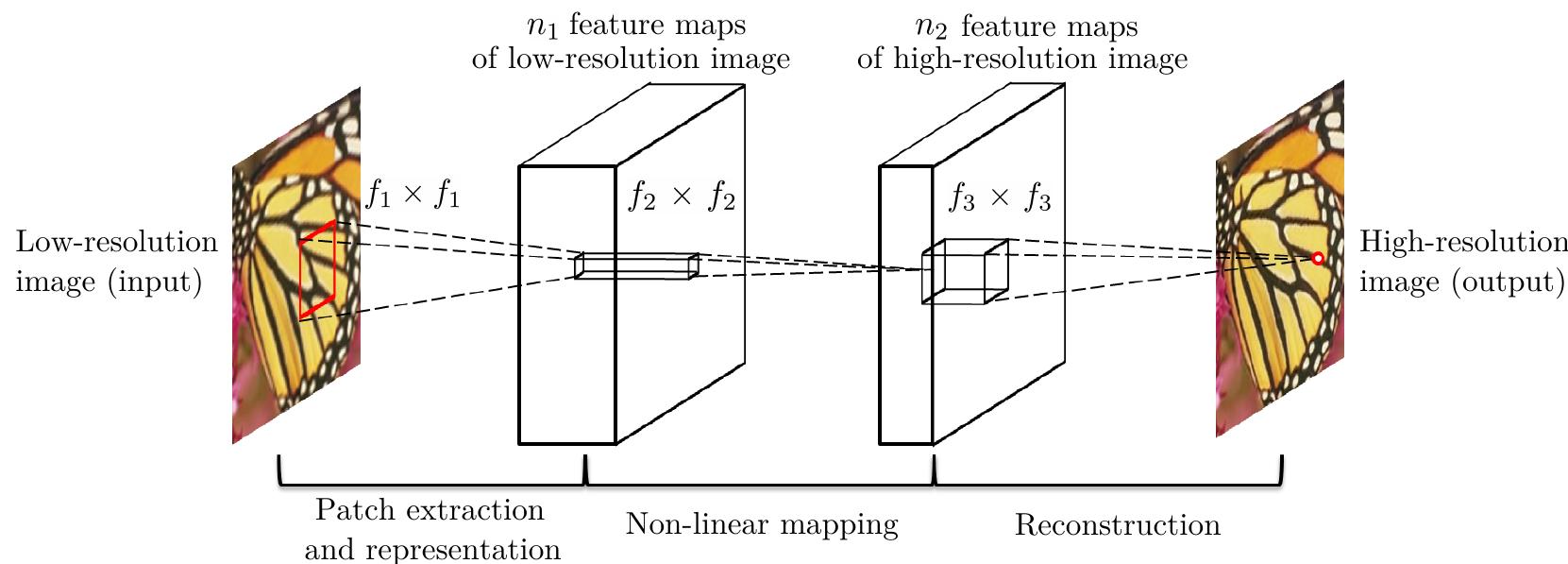
论文中的 SRCNN 网络结构

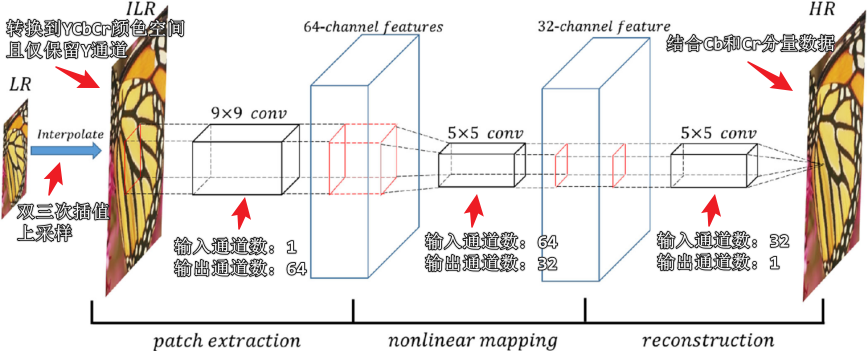
文中首先将 LR 利用双三次插值上采样得到了 input，接着按照上图的结构：

  • 首先是一个 \(f_1\times f_1\) 卷积 + ReLU 激活操作，学习提取 LR 特征的非线性映射函数；
  • 然后是一个 \(f_2\times f_2\) 卷积 + ReLU 激活操作，学习从 LR 特征到 HR 特征的非线性映射函数；
  • 最后是一个 \(f_3\times f_3\) 卷积操作，学习从 HR 特征重构到 HR 的线性映射函数。

SRCNN 网络结构解析

可以看出 SRCNN 仅包含卷积层且全部都是等宽卷积，不包含池化层和全连接层，SRCNN 使用 MSE 作为损失函数。整个网络的 PyTorch 代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class SRCNN(nn.Module):
    def __init__(self) -> None:
        super(SRCNN, self).__init__()
        # 1. ILR 特征提取层
        self.features = nn.Sequential(
            nn.Conv2d(
                in_channels=1,
                out_channels=64,
                kernel_size=(9, 9),
                stride=(1, 1),
                padding=(4, 4)
            ),
            nn.ReLU(True)
        )

        # 2. 非线性映射层
        self.map = nn.Sequential(
            nn.Conv2d(64, 32, (5, 5), (1, 1), (2, 2)),
            nn.ReLU(True)
        )

        # 3. SR 重构层
        self.reconstruction = nn.Conv2d(32, 1, (5, 5), (1, 1), (2, 2))

        # 随机初始化模型权重
        self._initialize_weights()

SRCNN 将 LR 图像的双三次插值结果作为 HR 图像的初始估计，这存在以下问题：

  • 双三次插值的细节平滑可能会导致网络对图像细节的错误估计；
  • 处理双三次插值后的图像的效率较低；
  • 退化核未知的情况下，使用固定的上采样算法作为初始估计并不合理。

更窄的 SRCNN

SRCNN 的网络第一步通过插值将 LR 图像转化为 ILR，使得网络参数量很大，并且这有着很强的假设在里面，即默认退化核是插值的逆过程。能否直接在 LR 上学习呢？答案是可以的。

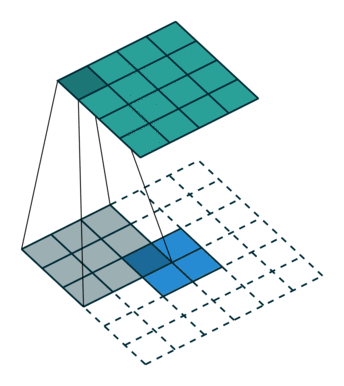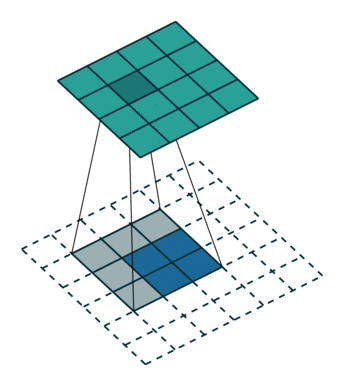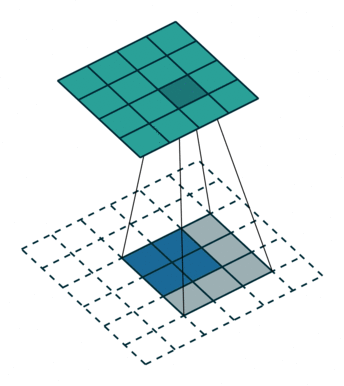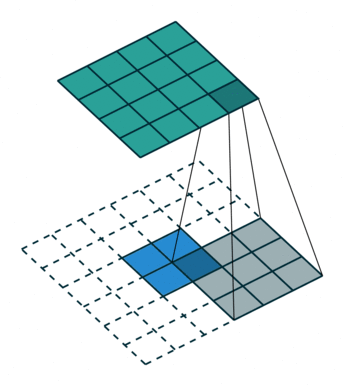
FSRCNN 3 网络采用了反卷积/转置卷积 4 策略，规避了 SRCNN 一开始的插值操作。转置卷积实例如下：

s = 1 时的转置卷积运算示例：

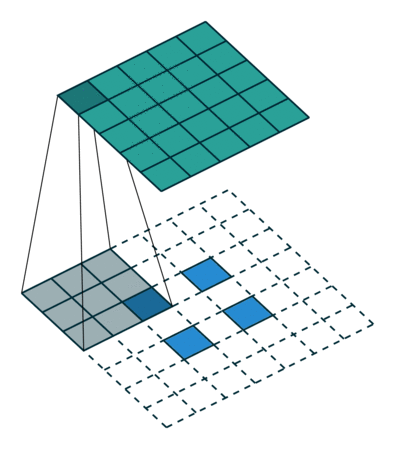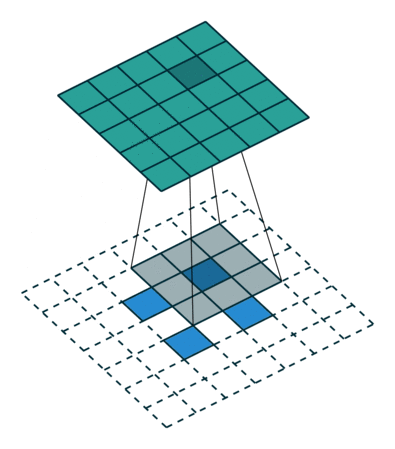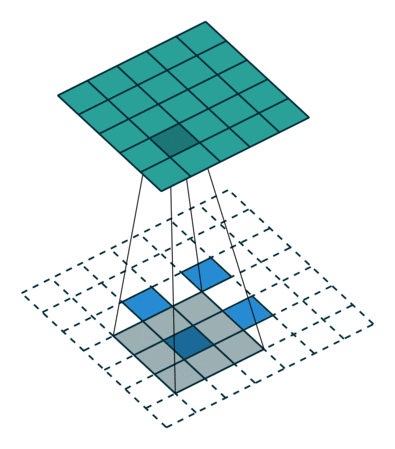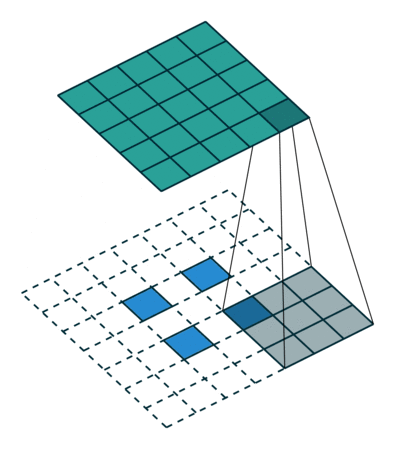
s = 1 时的转置卷积运算示例

s > 1 时的转置卷积运算示例：

s > 1 时的转置卷积运算示例

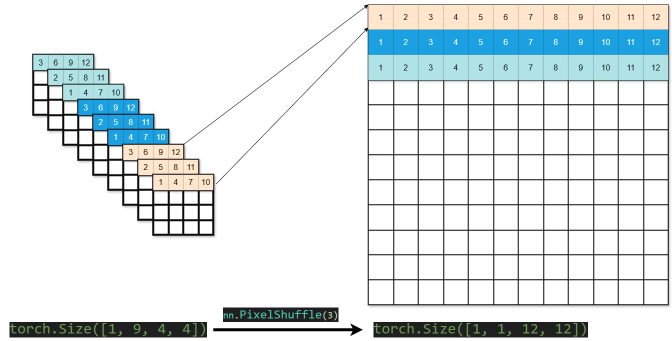
ESPCN 5 网络采用了亚像素卷积策略，同样规避了 SRCNN 一开始的插值操作。亚像素卷积实例如下：

上采样 3 倍的亚像素卷积

更深的 SRCNN

我们知道，一般情况下，只要能解决梯度消失和梯度爆炸问题，网络越深则性能越强，为此更深的网络被提了出来。

VDSR 6 网络主要有以下几个特点：

  1. 结构上：采用了 VGG Net 的思想，以块为单位搭建网络，并采用「残差连接」策略防止梯度消失；
  2. 训练上：为了进一步提高训练速度，VDSR 采用了更大的学习率，同时使用「梯度裁剪」策略防止梯度爆炸。梯度裁剪约束了参数的梯度变化值，要么约束上下界为定值，要么进行范数放缩；
  3. 训练上：采用了多尺度训练策略。VDSR 没有采用反卷积或亚像素卷积，仍然采用 SRCNN 的插值策略，因此不同尺度对 VDSR 没影响，直接插值到一样的尺度就行。

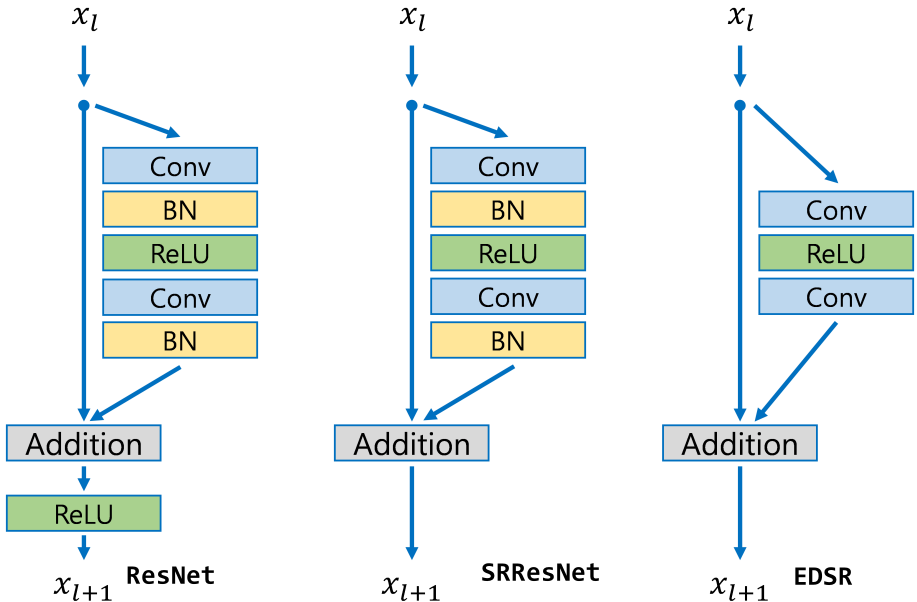
SRGAN 7 网络首次将 GAN 应用于超分任务，并基于残差结构提出了 SRResNet。

EDSR 8 网络在 SRResNet 的基础上改进了残差结构，去除了其中的 BN 层，节省了 40% 的内存，从而构建了更深的网络。同时，EDSR 认为不同尺度下的超分过程具有很强的相关性，所以提出了一种预训练策略，即在训练 \(\times 3\) 和 \(\times 4\) 的超分模型时，使用训练好的 \(\times 2\) 超分模型的参数作为初始值。

ResNet vs. SRResNet vs. EDSR

为什么超分任务不依赖 BN 操作？不妨先回看一下 GoogLeNet 引入 BN 的意义是什么：

  • 对于图像分类任务而言。BN 层起到了正则化的作用，有助于提高网络的泛化能力；同时，由于特征空间和标签空间分布差异大，需要 BN 层解决 Covariance Shift 问题；
  • 对于图像超分任务而言。图像超分辨率可以看作是像素的密集预测任务，图像中像素值的改变也会影响超分的结果（数据增强的方式一般只有水平翻转和旋转）；同时，超分任务的输入和输出的分布差异较小，不太需要调整特征的分布。

  1. Yang W, Zhang X, Tian Y, et al. Deep learning for single image super-resolution: A brief review[J]. IEEE Transactions on Multimedia, 2019, 21(12): 3106-3121. ↩

  2. Dong C, Loy C C, He K, et al. Learning a deep convolutional network for image super-resolution[C]//Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part IV 13. Springer International Publishing, 2014: 184-199. ↩

  3. Dong C, Loy C C, Tang X. Accelerating the super-resolution convolutional neural network[C]//Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part II 14. Springer International Publishing, 2016: 391-407. ↩

  4. Dumoulin V, Visin F. A guide to convolution arithmetic for deep learning[J]. arXiv preprint arXiv:1603.07285, 2016. ↩

  5. Shi W, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 1874-1883. ↩

  6. Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 1646-1654. ↩

  7. Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4681-4690. ↩

  8. Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of the IEEE conference on computer vision and pattern recognition workshops. 2017: 136-144. ↩